题目内容
函数 的递增区间是
的递增区间是
A. | B. | C. | D. |
A
解析试题分析:首先将函数化为 ,令t=2x-
,令t=2x- ,x增大,t增大,所以为求函数的增区间,须研究y=2sint的减区间。
,x增大,t增大,所以为求函数的增区间,须研究y=2sint的减区间。
由 得
得 ,所以k=0时得
,所以k=0时得 ,故选A。
,故选A。
考点:本题主要考查三角函数的单调性。
点评:易错题,复合函数的单调性判断,遵循内外层函数“同增异减”。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知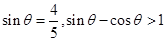 ,则
,则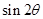 = ( )
= ( )
A.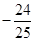 | B.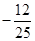 | C.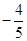 | D.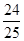 |
化简 等于
等于
A. | B. | C. | D. |
设函数 与函数
与函数 的对称轴完全相同,则
的对称轴完全相同,则 的值为( )
的值为( )
A. | B. | C. | D. |
若角 的终边上有一点
的终边上有一点 ,则
,则 的值是( )
的值是( )
A. | B. | C. | D. |
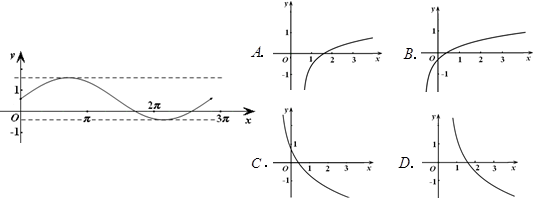
函数 的部分图象如图所示,则此函数的解析式为( )
的部分图象如图所示,则此函数的解析式为( )
A. | B. |
C. | D. |
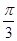 )的图像按
)的图像按 平移后得到g(x)图像,g(x)为偶函数,当|
平移后得到g(x)图像,g(x)为偶函数,当|


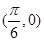
 是实数,则函数
是实数,则函数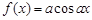 的图像可能是( )
的图像可能是( )
 的图像如图所示,则函数
的图像如图所示,则函数 的图像可能是( )
的图像可能是( )