题目内容
f(x)=sin(2x+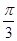 )的图像按
)的图像按 平移后得到g(x)图像,g(x)为偶函数,当|
平移后得到g(x)图像,g(x)为偶函数,当| |最小时,
|最小时, =
=
A. | B. | C. | D.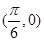 |
A
解析试题分析:因为已知函数f(x)=sin(2x+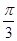 )的图像按
)的图像按 平移后得到g(x)图像,且g(x)为偶函数,那么当
平移后得到g(x)图像,且g(x)为偶函数,那么当 =
= 时,则向左平移
时,则向左平移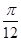 个单位,那么得到的表达式为f(x)=sin(2(x+
个单位,那么得到的表达式为f(x)=sin(2(x+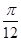 )+
)+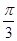 )=sin(2x+
)=sin(2x+ )=cos2x,满足题意可知成立。当
)=cos2x,满足题意可知成立。当 =
= 时,先向左移
时,先向左移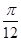 ,再向上平移1个单位,那么可知表达式为cos2x+1,但是模长不是最小的,
,再向上平移1个单位,那么可知表达式为cos2x+1,但是模长不是最小的,
当 =
=  此时不能满足偶函数的性质,因此不成立,同理可证当
此时不能满足偶函数的性质,因此不成立,同理可证当 =
=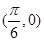 时,也不满足为偶函数,故选A.
时,也不满足为偶函数,故选A.
考点:本试题考查了三角函数图像的变换运用。
点评:解决该试题的关键是理解向量的坐标,表示的平移的方向,由于得到函数是偶函数,说明关于y轴对称,那么将诶和已知的关系式,可对选项逐一进行检验,然后得到结论,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
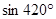 的值是 ( )
的值是 ( )
A.-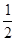 | B.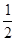 | C.-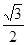 | D.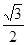 |
已知 ∈(
∈(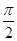 ,
, ),sin
),sin =
= ,则tan(
,则tan( )等于
)等于
| A.-7 | B.-  | C.7 | D. |
函数 ,函数
,函数 ,若存在
,若存在 ,使得
,使得 成立,则实数m的取值范围是
成立,则实数m的取值范围是
A. | B. | C. | D. |
要得到函数 的图象,只要将函数
的图象,只要将函数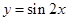 的图象( )
的图象( )
A.向左平移 单位 单位 | B.向右平移 单位 单位 |
C.向右平移 单位 单位 | D.向左平移 单位 单位 |
函数 的递增区间是
的递增区间是
A. | B. | C. | D. |
已知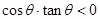 ,则角
,则角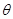 是( )
是( )
| A.第一象限角或第二象限角 | B.第二象限角或地三象限角 |
| C.第三象限角或第四象限角 | D.第四象限角或第一象限角 |
为了得到函数 的图像,只要把函数
的图像,只要把函数 图象上所有的点( )
图象上所有的点( )
A.向左平行移动 个单位长度 个单位长度 | B.向右平行移动 个单位 个单位 |
C.向左平行移动 个单位长度 个单位长度 | D.向右平行移动 个单位 个单位 |
已知 ,则角
,则角 的终边落在 ( )
的终边落在 ( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |