题目内容
若f(x)在x=0处连续,且x≠0时,f(x)=
,则f(0)=( )
| |||
|
分析:由题意可得,
f(x)=f(0),而对式子
可在分子分母上同时乘(
+1)(
+
+1)进行化简可求
| lim |
| x→0 |
| |||
|
| 1+x |
| 3 | (1-x)2 |
| 3 | 1-x |
解答:解:由题意可得,
f(x)=f(0)
∵
f(x)=
=
=
=
•
=
=-
故选A
| lim |
| x→0 |
∵
| lim |
| x→0 |
| lim |
| x→0 |
| |||
|
| lim |
| x→0 |
(
| |||||
(
|
=
| lim |
| x→0 |
| x | |||||
(
|
=
| lim |
| x→0 |
x(
| ||||||
| 1-x-1 |
| 1 | ||
|
=
| lim |
| x→0 |
-(
| ||||||
1+
|
=-
| 3 |
| 2 |
故选A
点评:本题主要考查了函数的连续的条件的应用,解题的关键是熟练应用函数连续的定义,解答本题的难点在于对所求式子的化简

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目

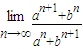 (a2+b2≠0且a≠-b);
(a2+b2≠0且a≠-b); .
.
 (m>0,m≠1,n≥2,n∈N*)若f(x)在x=0处连续,则m的值为
(m>0,m≠1,n≥2,n∈N*)若f(x)在x=0处连续,则m的值为

