题目内容
(1)①计算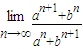 (a2+b2≠0且a≠-b);
(a2+b2≠0且a≠-b);②计算
 .
.(2)设函数

①若f(x)在x=0处的极限存在,求a,b的值;
②若f(x)在x=0处连续,求a,b的值.
【答案】分析:(1)①当a=b≠0,|a|>|b|和|a|<|b|时,根据题设条件和计算法则分别求解
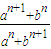 的值.
的值.
②分子分线同时除以x,把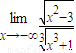 转化为
转化为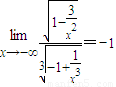 .
.
(2)①求出函数的左极限是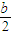 ,右极限是1.由f(x)在x=0处的极限存在,知
,右极限是1.由f(x)在x=0处的极限存在,知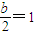 ,所以b=2.故a∈R,b=2.
,所以b=2.故a∈R,b=2.
②由f(x)在x=0处连续,知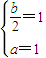 ,故a=1,b=2.
,故a=1,b=2.
解答:解:(1)①当a=b≠0时,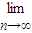
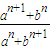 =1;
=1;
当|a|>|b|时,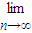
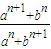 =
=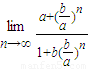 =a;
=a;
当|a|<|b|时,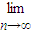
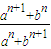 =
=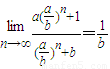 .
.
∴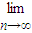
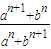 =
= .
.
② =
= .
.
(2)解:①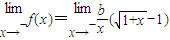
=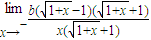
=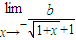
=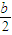 .
.
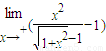 =
=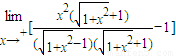
=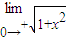 =1.
=1.
∵f(x)在x=0处的极限存在,∴ ,∴b=2.
,∴b=2.
故a∈R,b=2.
②∵f(x)在x=0处连续,∴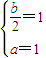 ,∴a=1,b=2.
,∴a=1,b=2.
点评:本题考查极限、迦续的概念和性质,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件.

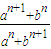 的值.
的值.②分子分线同时除以x,把
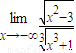 转化为
转化为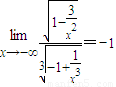 .
.(2)①求出函数的左极限是
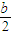 ,右极限是1.由f(x)在x=0处的极限存在,知
,右极限是1.由f(x)在x=0处的极限存在,知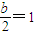 ,所以b=2.故a∈R,b=2.
,所以b=2.故a∈R,b=2.②由f(x)在x=0处连续,知
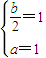 ,故a=1,b=2.
,故a=1,b=2.解答:解:(1)①当a=b≠0时,
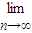
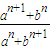 =1;
=1;当|a|>|b|时,
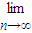
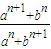 =
=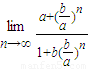 =a;
=a;当|a|<|b|时,
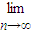
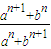 =
=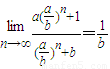 .
.∴
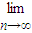
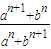 =
= .
.②
 =
= .
.(2)解:①
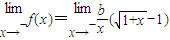
=
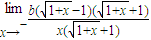
=
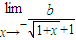
=
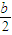 .
.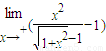 =
=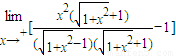
=
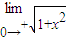 =1.
=1.∵f(x)在x=0处的极限存在,∴
 ,∴b=2.
,∴b=2.故a∈R,b=2.
②∵f(x)在x=0处连续,∴
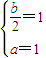 ,∴a=1,b=2.
,∴a=1,b=2.点评:本题考查极限、迦续的概念和性质,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件.

练习册系列答案
相关题目