题目内容

将函数f（x）=sin2x-cos2x的图象按向量
a
平移后所得图象关于y轴对称，则|
a
|的最小值为（　　）
A、
3π
8
B、
π
8
C、
3π
4
D、
π
4
分析：化简函数f（x）=sin2x-cos2x，然后平移使之为类似余弦函数，求出a的值，即可得到|
a
|的最小值．
解答：解：由题意可以令
a
=(a，0)函数f（x）=sin2x-cos2x=
2
sin（2x-
π
4
），图象按向量
a
平移后所得的图象关于y轴对称，
可得y=
2
sin[2（x-a）-
π
4
]，当a=-
π
8
，即
a
=（-
π
8
，0）时函数是偶函数，此时|
a
|最小，关于y轴对称．|
a
|=
π
8
．
故选B．
点评：本题考查函数y=Asin（ωx+φ）的图象变换，注意函数图象的平移只能是左右平移，是解题的关键，是基础题．
练习册系列答案
相关题目
已知向量a=(sinx•
3
)，b=(cosx•si
n
2
 
x-
1
2
)，函数f（x）=a•b．
（1）求f（x）单调递增区间；
（2）将函数f（x）图象按向量c=（m，0），得到函数y=g（x）的图象，且g（x）为偶函数，求正实数m的最小值．
已知函数f(x)=sin2ωx+
3
sinωxcosωx(ω＞0)的最小正周期为3π．
（1）将函数f（x）的图象向左平移
π
4
单位后得到函数g（x）的图象，求g（x）在区间[0，2π]上的值域；
（2）若sin(θ+ωπ)=
3
3
，且0＜θ＜
π
2
，求sinθ．
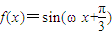函数（ω＞0）的图象的相邻两条对称轴间的距离是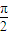．若将函数f（x）图象向右平移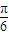个单位，得到函数g（x）的解析式为（ ）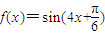
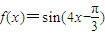
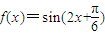
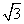A．
B．
C．
D．f（x）=sin2
已知函数f（x）=sin2ωx+sinωx·sin（ωx+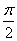）+2cos2ωx，x∈R（ω>0），在y轴右侧的第一个最高点的横坐标为。
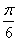（1）求ω；
（2）若将函数f（x）的图象向右平移个单位后，再将得到的图象上各点横坐标伸长到原来的4倍，纵坐标不变，得到函数y=g（x）的图象，求函数g（x）的最大值及单调递减区间。

将函数f （x）=sin2 x （x∈R）的图象向右平移个单位，则所得到的图象对应的函数的一个单调递增区间是                                                                                   （    ）

       A．（-，0）          B．（0，）    C．（，）       D．（，π）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网