题目内容
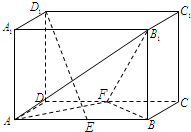
如图,矩形ABCD的对角线AC,BD交于O,AB=4,AD=3.沿AC把△ACD折起,使二面角D1-AC-B为直二面角.
(1)求直线AD1与直线DC所成角的余弦值;
(2)求二面角A-DD1-C的平面角正弦值大小.
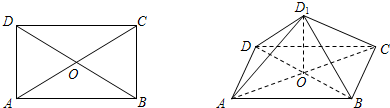
(1)求直线AD1与直线DC所成角的余弦值;
(2)求二面角A-DD1-C的平面角正弦值大小.
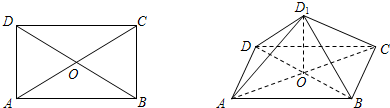
(1)以点B为坐标原点,平面ABC为xOy平面,BC,BA方向分别为x轴,y轴的正方向,建立空间直角坐标系.则B(0,0,0),C(3,0,0),A(0,4,0).
在矩形ABCD中,作DH⊥AC于H,HM⊥BC于M,HN⊥AB于N,则H即为D1在平面ABC上的射影.
∵AB=4,AD=3,∴AC=5,DH=
,HN=
,HM=
,D1(
,
,
),…(6分)
∴
=(
,
,
)-(0,4,0)=(
,
,
),
=(3,0,0)-(3,4,0)=(0,-4,0),
所以cos<
,
>=
=
.…(10分)
(2)设平面D1BC的法向量为
=(a,b,c),
=(3,0,0),
=(0,4,0),
∵
•
=0,
•
=0,∴
∴
=(0,-15,16).
设平面D1BA的法向量为
=(x,y,z),
∵
•
=0,
•
=0,
∴
,∴
=(-20,0,-9).…(14分)
∴cos<
,
>=
=-
,
∴sinθ=
=
.…(16分)
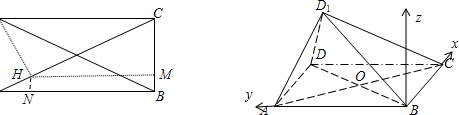
在矩形ABCD中,作DH⊥AC于H,HM⊥BC于M,HN⊥AB于N,则H即为D1在平面ABC上的射影.
∵AB=4,AD=3,∴AC=5,DH=
| 12 |
| 5 |
| 27 |
| 25 |
| 64 |
| 25 |
| 27 |
| 25 |
| 64 |
| 25 |
| 12 |
| 5 |
∴
| AD1 |
| 27 |
| 25 |
| 64 |
| 25 |
| 12 |
| 5 |
| 27 |
| 25 |
| -36 |
| 25 |
| 12 |
| 5 |
| DC |
所以cos<
| AD1 |
| DC |
| ||||
|
|
| 12 |
| 25 |
(2)设平面D1BC的法向量为
| n |
| BC |
| BA |
∵
| n |
| BC |
| n |
| D1B |
|
| n |
设平面D1BA的法向量为
| m |
∵
| m |
| BA |
| m |
| D1B |
∴
|
| m |
∴cos<
| m |
| n |
| ||||
|
|
| 144 |
| 481 |
∴sinθ=
1-(
|
25
| ||
| 481 |
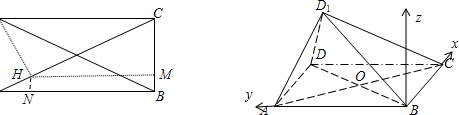

练习册系列答案
相关题目