题目内容
18.已知函数f(x)=|x+1|+|x+2|+|x-1|+|x-2|,且f(a2-3a+2)=f(a-1),则满足条件的所有整数a的和是6.分析 根据已知中f(x)=|x+1|+|x+2|+|x-1|+|x-2|,结合函数奇偶性的定义,我们可以求出函数为一个偶函数,则f(a2-3a+2)=f(a-1),可以转化为|a2-3a+2|=|a-1|,又由绝对值的几何意义,我们可得f(0)=f(1)=f(-1),可知a=2也满足要求,进而得到答案.
解答 解:∵函数f(x)=|x+1|+|x+2|+|x-1|+|x-2|,
∴f(-x)=|-x+1|+|-x+2|+|-x-1|+|-x-2|=|x-1|+|x-2|+|x+1|+|x+2|,
即函数f(x)为偶函数
若f(a2-3a+2)=f(a-1),
则a2-3a+2=a-1,或a2-3a+2=-(a-1)
即a2-4a+3=0,或a2-2a+1=0
解得a=1,或a=3
又∵f(0)=f(1)=f(-1)
∴当a=2时,也满足要求,
故满足条件的所有整数a的和是1+2+3=6,
故答案为:6.
点评 本题考查的知识点是函数奇偶性的性质,及绝对值的几何意义,解答本题的技巧性较强,难度也比较大,其中分析出函数的奇偶性,从面将f(a2-3a+2)=f(a-1),转化为一个绝对值方程是解答本题的关键,但易忽略f(0)=f(1)=f(-1),而错解为4.

练习册系列答案
相关题目
9.已知全集U=R,集合A={x|x2-4≥0},B={x|0≤x<5},则(∁UA)∩B=( )
| A. | (0,2) | B. | (0,2] | C. | [0,2) | D. | [-2,2] |
6.某几何体的三视图如图所示,则该三视图的体积为( )
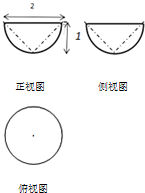

| A. | $\frac{π}{3}$ | B. | $\frac{4}{3}$π | C. | 2π | D. | $\frac{8}{3}$π |
13.已知直线x+ay+2=0(a∈R)与圆x2+y2+2x-2y+1=0相切,则a的值为( )
| A. | 1 | B. | -1 | C. | 0 | D. | 0或1 |
3.△ABC中,角A,B,C的对边分别是a,b,c,已知a=b,c2=2b2(1-sinC),则C=( )
| A. | $\frac{3π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |