题目内容
已知函数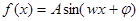 ,
,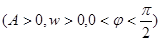 图象与x轴交点中,相邻两个交点之间的距离为
图象与x轴交点中,相邻两个交点之间的距离为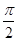 ,且图象最低点
,且图象最低点
(1)求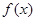 解析式
解析式
(2)将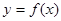 所有点纵坐标缩短到原来的
所有点纵坐标缩短到原来的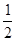 倍(横坐标不变),在将图象向右平移
倍(横坐标不变),在将图象向右平移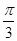 个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到
个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到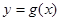 ,求
,求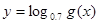 的单调递减区间
的单调递减区间
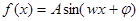 ,
,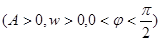 图象与x轴交点中,相邻两个交点之间的距离为
图象与x轴交点中,相邻两个交点之间的距离为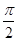 ,且图象最低点
,且图象最低点
(1)求
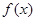 解析式
解析式(2)将
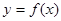 所有点纵坐标缩短到原来的
所有点纵坐标缩短到原来的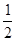 倍(横坐标不变),在将图象向右平移
倍(横坐标不变),在将图象向右平移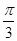 个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到
个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到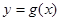 ,求
,求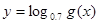 的单调递减区间
的单调递减区间(1)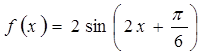 (2)
(2)
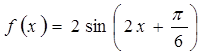 (2)
(2)
本试题主要是考查了三角函数的图像与解析式的关系,以及函数的单调区间和图像变换的综合运用。
(1)由于由已知得相邻两个交点之间的距离为 则周期T=
则周期T= ,得到w,A的值,然后代点得到
,得到w,A的值,然后代点得到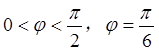 的值,得到解析式。
的值,得到解析式。
(2)因为将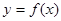 所有点纵坐标缩短到原来的
所有点纵坐标缩短到原来的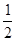 倍(横坐标不变),在将图象向右平移
倍(横坐标不变),在将图象向右平移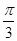 个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到
个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到 然后结合对数的性质得到单调区间。
然后结合对数的性质得到单调区间。
由已知得相邻两个交点之间的距离为 则周期T=
则周期T=
解得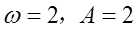 ,图象最低点M
,图象最低点M 得
得
 ,
,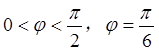
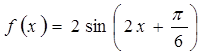 (4分)
(4分)
(2)由图象变换知 (6 分)
(6 分)
先求定义域令g(x)>0 即 >0,
>0, 解得x 的范围是
解得x 的范围是 (8分)
(8分)
求函数的单调递减区间,由复合函数的单调性同增异减知
需要求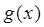 的单调递增区间,即求
的单调递增区间,即求 的单调递减区间解得x的范围是
的单调递减区间解得x的范围是 (10分)
(10分)
则 的单调递减区间为
的单调递减区间为

(1)由于由已知得相邻两个交点之间的距离为
 则周期T=
则周期T= ,得到w,A的值,然后代点得到
,得到w,A的值,然后代点得到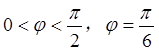 的值,得到解析式。
的值,得到解析式。(2)因为将
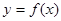 所有点纵坐标缩短到原来的
所有点纵坐标缩短到原来的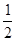 倍(横坐标不变),在将图象向右平移
倍(横坐标不变),在将图象向右平移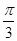 个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到
个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到 然后结合对数的性质得到单调区间。
然后结合对数的性质得到单调区间。由已知得相邻两个交点之间的距离为
 则周期T=
则周期T=
解得
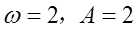 ,图象最低点M
,图象最低点M 得
得
 ,
,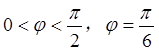
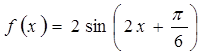 (4分)
(4分)(2)由图象变换知
 (6 分)
(6 分)先求定义域令g(x)>0 即
 >0,
>0, 解得x 的范围是
解得x 的范围是 (8分)
(8分)求函数的单调递减区间,由复合函数的单调性同增异减知
需要求
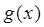 的单调递增区间,即求
的单调递增区间,即求 的单调递减区间解得x的范围是
的单调递减区间解得x的范围是 (10分)
(10分)则
 的单调递减区间为
的单调递减区间为

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 是第二象限角,角
是第二象限角,角 ,且
,且 ,则
,则 =
=



 为始边作角
为始边作角 与
与 (
( ,它们的终边分别与单位圆相交于点
,它们的终边分别与单位圆相交于点 、
、 ,已知点
,已知点 .
.
 的值;
的值; ,求
,求 .
.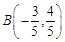 ,点C为⊙O与
,点C为⊙O与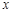 轴正半轴的交点,设∠COB=θ.
轴正半轴的交点,设∠COB=θ.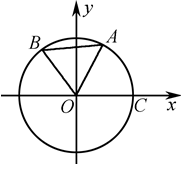
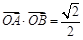 ,求点A的横坐标xA.
,求点A的横坐标xA. 的圆心角所对的弧的长度为( )
的圆心角所对的弧的长度为( )


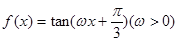 图象中的两条相邻“平行曲线”与直线y =2012相交于A,B两点,且|AB| =2,则
图象中的两条相邻“平行曲线”与直线y =2012相交于A,B两点,且|AB| =2,则 )=
)=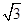

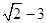
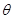 ,那么
,那么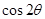 的值为 ;
的值为 ;




 ,则
,则 。
。