题目内容
如图，以
为始边作角
与
（
，它们的终边分别与单位圆相交于点
、
，已知点的坐标为
.
（Ⅰ）求
的值；
（Ⅱ）若
，求
．
为始边作角与（，它们的终边分别与单位圆相交于点、，已知点的坐标为.（Ⅰ）求
的值；（Ⅱ）若
，求．解：（Ⅰ）由三角函数定义知：
，
，
所以
，
．
所以
． ………………………3分
（Ⅱ）若，则
，由
得
，
………………………6分
，，所以
，．所以
． ………………………3分（Ⅱ）若
，则，由得，………………………6分经历用向量的数量积推导出题目要用的条件的过程，体验和感受数学发现和创造的过程，体会向量和三角函数的联系；高考题目中向量和三角函数经常结合在一起出现
（1）根据三角函数定义得到角的三角函数值，把要求的式子化简用二倍角公式，切化弦，约分整理代入数值求解．
（2）以向量的数量积为0为条件，得到垂直关系，在角上表现为差是90°用诱导公式求解．
（1）根据三角函数定义得到角的三角函数值，把要求的式子化简用二倍角公式，切化弦，约分整理代入数值求解．
（2）以向量的数量积为0为条件，得到垂直关系，在角上表现为差是90°用诱导公式求解．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
，
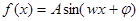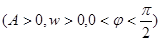图象与x轴交点中，相邻两个交点之间的距离为
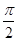，且图象最低点
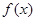解析式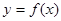
所有点纵坐标缩短到原来的
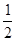倍（横坐标不变），在将图象向右平移
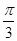个单位长度，最后在将所有点横坐标伸长到原来4倍（纵坐标不变）得到
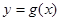，求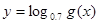
的单调递减区间
的最大值为（ ）
是第一象限角，则
的值与1的大小关系是
，面积为
，求扇形的圆心角的弧度数 
的终边经过点P
,求角
角的正弦，余弦与正切.
，
的最大值为（ ）
终边上一点坐标为
，则
_________.