题目内容
(本小题满分14分)
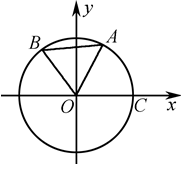
如图,O为坐标原点,点A,B在⊙O上,且点A在第一象限,点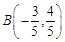 ,点C为⊙O与
,点C为⊙O与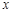 轴正半轴的交点,设∠COB=θ.
轴正半轴的交点,设∠COB=θ.
(1) 求sin2θ的值;
(2) 若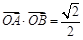 ,求点A的横坐标xA.
,求点A的横坐标xA.
如图,O为坐标原点,点A,B在⊙O上,且点A在第一象限,点
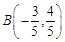 ,点C为⊙O与
,点C为⊙O与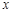 轴正半轴的交点,设∠COB=θ.
轴正半轴的交点,设∠COB=θ.
(1) 求sin2θ的值;
(2) 若
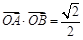 ,求点A的横坐标xA.
,求点A的横坐标xA.(1) sin2θ=2sinθcosθ=-.
(2)点A的横坐标 .
.
(2)点A的横坐标
 .
. 本试题主要是考查了的三角函数的定义和三角函数的两角和差的公式,以及向量的数量积公式的运用。
(1)因点C在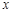 轴正半轴上,点
轴正半轴上,点 ,∠
,∠ ,
,
所以由三角函数定义知cosθ=-,sinθ=
(2)因为 ,又
,又  ,
,
所以 ,由题意可知∠BOA=45°
,由题意可知∠BOA=45°
然后结合 公式得到结论。
公式得到结论。
(1) 因点C在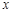 轴正半轴上,点
轴正半轴上,点 ,∠
,∠ ,
,
所以由三角函数定义知cosθ=-,sinθ=,………3分
所以sin2θ=2sinθcosθ=-.………………………6分
(2) 因为 ,又
,又  ,
,
所以 ,由题意可知∠BOA=45°,…………………………………………9分
,由题意可知∠BOA=45°,…………………………………………9分
又∠ ,所以
,所以 ,
,
而 =
= .…………………………………………12分
.…………………………………………12分
故点A的横坐标 . ……………………………………14分
. ……………………………………14分
(1)因点C在
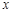 轴正半轴上,点
轴正半轴上,点 ,∠
,∠ ,
,所以由三角函数定义知cosθ=-,sinθ=
(2)因为
 ,又
,又  ,
,所以
 ,由题意可知∠BOA=45°
,由题意可知∠BOA=45°然后结合
 公式得到结论。
公式得到结论。(1) 因点C在
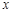 轴正半轴上,点
轴正半轴上,点 ,∠
,∠ ,
,所以由三角函数定义知cosθ=-,sinθ=,………3分
所以sin2θ=2sinθcosθ=-.………………………6分
(2) 因为
 ,又
,又  ,
,所以
 ,由题意可知∠BOA=45°,…………………………………………9分
,由题意可知∠BOA=45°,…………………………………………9分又∠
 ,所以
,所以 ,
,而
 =
= .…………………………………………12分
.…………………………………………12分故点A的横坐标
 . ……………………………………14分
. ……………………………………14分
练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
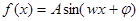 ,
,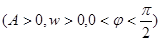 图象与x轴交点中,相邻两个交点之间的距离为
图象与x轴交点中,相邻两个交点之间的距离为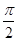 ,且图象最低点
,且图象最低点
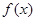 解析式
解析式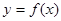 所有点纵坐标缩短到原来的
所有点纵坐标缩短到原来的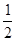 倍(横坐标不变),在将图象向右平移
倍(横坐标不变),在将图象向右平移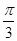 个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到
个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到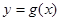 ,求
,求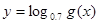 的单调递减区间
的单调递减区间 = .
= . 是第一象限角,则
是第一象限角,则 的值与1的大小关系是
的值与1的大小关系是


 的终边经过点P
的终边经过点P ,求角
,求角



 ,则2a是( )
,则2a是( ) .
.