题目内容
【题目】如图,已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.
,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N. 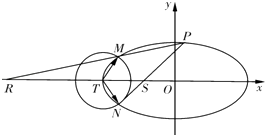
(1)求椭圆C的方程;
(2)求 ![]() 的最小值,并求此时圆T的方程;
的最小值,并求此时圆T的方程;
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:|OR||OS|为定值.
【答案】
(1)解:依题意,得a=2, ![]() ,
,
∴c= ![]() ,b=
,b= ![]() =1,
=1,
故椭圆C的方程为 ![]() .
.
(2)解:方法一:点M与点N关于x轴对称,
设M(x1,y1),N(x1,﹣y1),不妨设y1>0.
由于点M在椭圆C上,所以 ![]() . (*)
. (*)
由已知T(﹣2,0),则 ![]() ,
, ![]() ,
,
∴ ![]()
=(x1+2)2﹣ ![]()
= ![]()
= ![]() .
.
由于﹣2<x1<2,
故当 ![]() 时,
时, ![]() 取得最小值为
取得最小值为 ![]() .
.
由(*)式, ![]() ,故
,故 ![]() ,
,
又点M在圆T上,代入圆的方程得到 ![]() .
.
故圆T的方程为: ![]() .
.
方法二:点M与点N关于x轴对称,
故设M(2cosθ,sinθ),N(2cosθ,﹣sinθ),
不妨设sinθ>0,由已知T(﹣2,0),
则 ![]()
=(2cosθ+2)2﹣sin2θ
=5cos2θ+8cosθ+3
= ![]() .
.
故当 ![]() 时,
时, ![]() 取得最小值为
取得最小值为 ![]() ,
,
此时 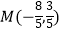 ,
,
又点M在圆T上,代入圆的方程得到 ![]() .
.
故圆T的方程为: ![]()
(3)解:方法一:设P(x0,y0),
则直线MP的方程为: ![]() ,
,
令y=0,得 ![]() ,
,
同理: ![]() ,
,
故 ![]() (**)
(**)
又点M与点P在椭圆上,
故 ![]() ,
, ![]() ,
,
代入(**)式,
得: ![]() .
.
所以|OR||OS|=|xR||xS|=|xRxS|=4为定值.
方法二:设M(2cosθ,sinθ),N(2cosθ,﹣sinθ),
不妨设sinθ>0,P(2cosα,sinα),其中sinα≠±sinθ.
则直线MP的方程为: ![]() ,
,
令y=0,得 ![]() ,
,
同理: ![]() ,
,
故 ![]() .
.
所以|OR||OS|=|xR||xS|=|xRxS|=4为定值
【解析】(1)依题意,得a=2, ![]() ,由此能求出椭圆C的方程.(2)法一:点M与点N关于x轴对称,设M(x1 , y1),N(x1 , ﹣y1),设y1>0.由于点M在椭圆C上,故
,由此能求出椭圆C的方程.(2)法一:点M与点N关于x轴对称,设M(x1 , y1),N(x1 , ﹣y1),设y1>0.由于点M在椭圆C上,故 ![]() .由T(﹣2,0),知
.由T(﹣2,0),知 ![]() =
= ![]() ,由此能求出圆T的方程. 法二:点M与点N关于x轴对称,故设M(2cosθ,sinθ),N(2cosθ,﹣sinθ),设sinθ>0,由T(﹣2,0),得
,由此能求出圆T的方程. 法二:点M与点N关于x轴对称,故设M(2cosθ,sinθ),N(2cosθ,﹣sinθ),设sinθ>0,由T(﹣2,0),得 ![]() =
= ![]() ,由此能求出圆T的方程.(3)法一:设P(x0 , y0),则直线MP的方程为:
,由此能求出圆T的方程.(3)法一:设P(x0 , y0),则直线MP的方程为: ![]() ,令y=0,得
,令y=0,得 ![]() ,同理:
,同理: ![]() ,故
,故 ![]() ,由此能够证明|OR||OS|=|xR||xS|=|xRxS|=4为定值.
,由此能够证明|OR||OS|=|xR||xS|=|xRxS|=4为定值.
法二:设M(2cosθ,sinθ),N(2cosθ,﹣sinθ),设sinθ>0,P(2cosα,sinα),其中sinα≠±sinθ.则直线MP的方程为: ![]() ,由此能够证明|OR||OS|=|xR||xS|=|xRxS|=4为定值.
,由此能够证明|OR||OS|=|xR||xS|=|xRxS|=4为定值.

 教材全解字词句篇系列答案
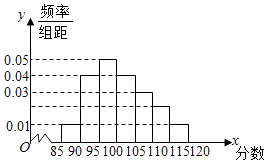
教材全解字词句篇系列答案【题目】某校高二奥赛班N名学生的物理测评成绩(满分120分)分布直方图如图,已知分数在100~110的学生数有21人. (Ⅰ)求总人数N和分数在110~115分的人数n;
(Ⅱ)现准备从分数在110~115分的n名学生(女生占 ![]() )中任选2人,求其中恰好含有一名女生的概率;
)中任选2人,求其中恰好含有一名女生的概率;
(Ⅲ)为了分析某个学生的学习状态,对其下一阶段的学习提供指导性建议,对他前7次考试的数学成绩x(满分150分),物理成绩y进行分析,下面是该生7次考试的成绩.
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩y与数学成绩x是线性相关的,若该生的数学成绩达到130分,请你估计他的物理成绩大约是多少?
附:对于一组数据(u1 , v1),(u2 , v2),,(un , vn),其回归线v=α+βu的斜率和截距的最小二乘估计分别为 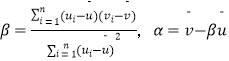 .
.