题目内容
抛物线y2=4x上一点M(x,y)到焦点的距离为3,则x=( )A.0
B.
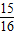
C.1
D.2
【答案】分析:根据抛物线y2=4x可知p=2,准线方程为x=-1,进而根据抛物线的定义可知点P到其焦点的距离等于点到其准线x=-1的距离,求得点的横坐标x.
解答:解:根据抛物线的方程y2=4x,可知p=2
根据抛物线的定义可知点到其焦点的距离等于点到其准线x=-1的距离,
所以x-(-1)=3,得x=2,
故选D.
点评:本题考查抛物线的定义,抛物线上的点到焦点的距离,叫焦半径.到焦点的距离常转化为到准线的距离求解.
解答:解:根据抛物线的方程y2=4x,可知p=2
根据抛物线的定义可知点到其焦点的距离等于点到其准线x=-1的距离,
所以x-(-1)=3,得x=2,
故选D.
点评:本题考查抛物线的定义,抛物线上的点到焦点的距离,叫焦半径.到焦点的距离常转化为到准线的距离求解.

练习册系列答案
相关题目