题目内容
在 中,角
中,角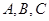 所对的边分别为
所对的边分别为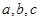 ,设
,设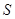 为
为 的面积,满足
的面积,满足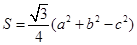 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)求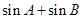 的最大值.
的最大值.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) 。
。
解析试题分析:(Ⅰ)由题意可知 absinC=
absinC= ,2abcosC. 所以tanC=
,2abcosC. 所以tanC= .因为0<C<
.因为0<C< ,所以C=
,所以C= .
.
(Ⅱ)由已知
sinA+sinB=sinA+sin( -C-A)=sinA+sin(
-C-A)=sinA+sin( -A)=sinA+
-A)=sinA+ cosA+
cosA+ sinA=
sinA= sin(A+
sin(A+ )≤
)≤ .
.
当△ABC为正三角形时取等号,所以sinA+sinB的最大值是 .
.
考点:余弦定理;三角形的面积公式;三角形内的隐含条件;诱导公式;三角恒等变换。
点评:三角函数的最值是三角函数中最基本的内容,也是历年高考命题的热点。对这类问题只要我们找到恰当的方法,就可以快速地求解。一般情况下要化为 的形式。
的形式。

练习册系列答案
相关题目
 中,D为BC边上一点,
中,D为BC边上一点, ,
,
 求AD.
求AD. 中,角
中,角 的对边长分别为
的对边长分别为 ,
, ,且
,且
 ;
;
 中,角A,B,C的对边分别是
中,角A,B,C的对边分别是 ,已知向量
,已知向量 ,
, ,且
,且 。
。 ,求
,求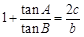 .
.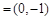 ,n
,n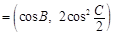 ,试求|m
,试求|m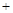 n|的最小值.
n|的最小值.  中,内角
中,内角 的对边分别为
的对边分别为 。若
。若 。(1)证明:
。(1)证明: ;(2)求
;(2)求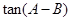 的最大值。
的最大值。 中,
中,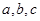 分别为内角
分别为内角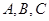 的对边,且
的对边,且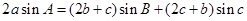 .
.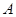
 的大小;
的大小;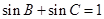 ,试判断
,试判断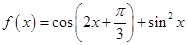 ,
,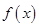 的最大值和最小正周期.,
的最大值和最小正周期.,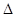 ABC的三个内角,若
ABC的三个内角,若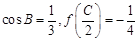 ,且C为锐角,求
,且C为锐角,求