题目内容
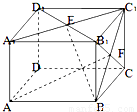
在长方体AC1中,AB=4,BC=CC1=2
.M是BC1的中点,N是MC1的中点,则异面直线AN与CM所成的角为
| 2 |
90°
90°
.分析:以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线AN与CM所成的角的大小.
解答: 解:以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,
解:以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,
∵长方体AC1中,AB=4,BC=CC1=2
.M是BC1的中点,N是MC1的中点,
∴A(2
,0,0),N(
,4,
),C(0,4,0),M(
,4,
),
∴
=(-
,4,
),
=(
,0,
),
设异面直线AN与CM所成的角为θ,
则cosθ=|cos<
,
>|=|
|=0,
∴θ=90°,
所以异面直线AN与CM所成的角为90°.
故答案为:90°.
 解:以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,
解:以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,∵长方体AC1中,AB=4,BC=CC1=2
| 2 |
∴A(2
| 2 |
| ||
| 2 |
3
| ||
| 2 |
| 2 |
| 2 |
∴
| AN |
3
| ||
| 2 |
3
| ||
| 2 |
| CM |
| 2 |
| 2 |
设异面直线AN与CM所成的角为θ,
则cosθ=|cos<
| AN |
| CM |
| -3+0+3 |
| 5×2 |
∴θ=90°,
所以异面直线AN与CM所成的角为90°.
故答案为:90°.
点评:本题考查异面直线所成角的大小的求法,解题时要认真审题,仔细解答,注意向量法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在长方体AC1中,AB=BC=2,
如图,在长方体AC1中,AB=BC=2, 长方体AC1中,AB=BC=1,AA1=2,过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于
长方体AC1中,AB=BC=1,AA1=2,过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于 ,这样的直线最多可作 ______条.
,这样的直线最多可作 ______条.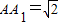 ,E,F分别是面A1C1.面BC1的中心,则AF和BE所成的角为( )
,E,F分别是面A1C1.面BC1的中心,则AF和BE所成的角为( )