题目内容
设△ABC的三边长分别为a、b、c，△ABC的面积为S，内切圆半径为，则r=
．类比这个结论可知：四面体A-BCD的四个面分别为S1、S2、S3、S4，内切球半径为R，四面体A-BCD的体积为V，则R=______．
| 2S |
| a+b+c |
设四面体的内切球的球心为O，
则球心O到四个面的距离都是R，
所以四面体的体积等于以O为顶点，
分别以四个面为底面的4个三棱锥体积的和．
则四面体的体积为 V四面体A-BCD=
| 1 |
| 3 |
则R=
| 3V |
| S1+S2+S3 |
故答案为：
| 3V |
| S1+S2+S3 |
练习册系列答案
孟建平名校考卷系列答案
相关题目
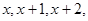则“△ABC是钝角三角形”的一个必要而不充分条件是 （
）
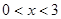B．
C．
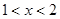D．
+
+
-
=________．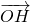