题目内容
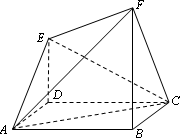
如图，已知
平面
是正三角形，
且
.
（1）设
是线段
的中点，求证：
∥平面
；
（2）求直线
与平面
所成角的余弦值.
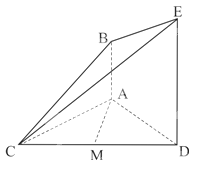
（I）证明：取CE中点N,连接MN,BN
则MN∥DE∥AB且MN=
DE=AB
∴四边形ABNM为平行四边形∴AM∥BN
∴AM∥平面BCE
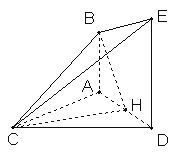
（Ⅱ）解：取AD中点H,连接BH，
∵
是正三角形， ∴CH⊥AD
又∵
平面
∴CH⊥AB ∴CH⊥平面ABED
∴∠CBH为直线 与平面所成的角
设AB=a,则AC=AD=2a , ∴BH=
a BC=
a
cos∠CBH=
……………
练习册系列答案
相关题目
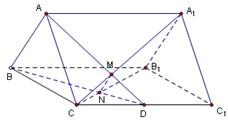如图，已知正三棱柱ABC-A1B1C1的底面边长是2，D是侧棱CC1的中点，平面ABD和平面A1B1C的交线为MN．
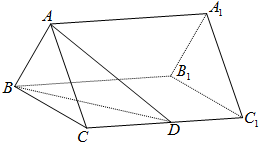如图，已知正三棱柱ABC-A1B1C1的底面边长是2，D是侧棱CC1的中点，直线AD与侧面BB1C1C所成的角为45°．
如图，已知ABCD是正方形，DE⊥平面ABCD，BF⊥平面ABCD，且AB=FB=2DE．
