Question

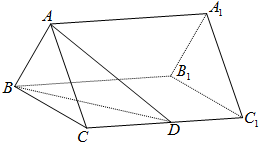如图，已知正三棱柱ABC-A₁B₁C₁的底面边长是2，D是侧棱CC₁的中点，直线AD与侧面BB₁C₁C所成的角为45°．
（1）求此正三棱柱的侧棱长；
（2）求二面角A-BD-C的平面角的正切值．

Answer 1

分析：（1）取BC中点E，连AE，ED，由正三棱柱的几何特征及面面垂直的性质，可得AE⊥侧面B₁C₁CB，则直线AD与侧面B₁C₁CB所成的角为∠ADE，解Rt△AED可得此正三棱柱的侧棱长
（2）过E作EF⊥BD于F，连AF，可得∠AFE为二面角A-BD-C的平面角，解Rt△BEF和Rt△AEF可得二面角A-BD-C的平面角的正切值．

解答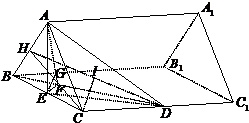：解：（1）设正三棱柱ABC-A₁B₁C₁的侧棱长为x．取BC中点E，连AE．
∵△ABC是正三角形，
∴AE⊥BC．
又底面ABC⊥侧面B₁C₁CB，且交线为BC．
∴AE⊥侧面B₁C₁CB，
连ED，则直线AD与侧面B₁C₁CB所成的角为∠ADE=45°．
在Rt△AED中，tan45°=

AE

ED

=

3

1+ x2 4

，
解得x=2

2

． 
∴此正三棱柱的侧棱长为2

2

．
（2）过E作EF⊥BD于F，连AF，
∵AE⊥侧面B₁C₁CB
∴AF⊥BD
∴∠AFE为二面角A-BD-C的平面角．
在Rt△BEF中，EF=BEsin∠EBF，又
BE=1，sin∠EBF=

CD

BC

=

2

22+ 2 3

=

3

3

∴EF=

3

3

．
又AE=

3

∴在Rt△AEF中，
tan∠AFE=

AE

EF

=3
即二面角A-BD-C的平面角的正切值为3

点评：本题考查的知识点是正三棱柱的几何特征，二面角的平面角及求法，其中找出已知的线面夹角的平面角及未知的二面角的平面角是解答的关键．