题目内容
如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.
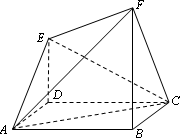
(Ⅰ)求证:平面AEC⊥平面AFC;
(Ⅱ)求直线EC与平面BCF所成的角;
(Ⅲ)问在EF上是否存在一点M,使三棱锥M-ACF是正三棱锥?
若存在,试确定M点的位置;若不存在,请说明理由.
解析:
解:(Ⅰ)连结BD,AC,设他们交于点O,连结EO,FO,
∵ABCD是正方形,∴OD⊥AC.
又∵ED⊥平面ABCD,且OD为ED在平面ABCD内的射影
∴EO⊥AC.同理FO⊥AC,
∴∠EOF就是二面角E-AC-F的平面角.
设DE=![]() ,∵AB=BF=2DE
,∵AB=BF=2DE![]() ,
,
∴OE=![]() ,OF=
,OF=![]() ,EF=
,EF=![]() .
.
∴EO2+FO2=EF2,即![]() ,∴平面AEC⊥平面AFC.
,∴平面AEC⊥平面AFC.
[另法提示:建立空间直角坐标系,证![]() ]
]
(Ⅱ)过点C作CP⊥平面AC,且使CP=DE,连结EP,则四边形CDEP是矩形,且CP在平面FBC内,∵DC![]() 平面FBC,EP∥DC,∴EP⊥平面FBC,
平面FBC,EP∥DC,∴EP⊥平面FBC,
∴∠ECP就是EC与平面FBC所成的角,
在Rt△ECP中,EP=2a,CP=a,∴tan∠ECP=2,
∴EC与平面FBC所成的角为arctan2.
[另法提示:一、转化为求EC与平面ADE所成的角;二、利用空间向量求解,先求![]() 与平面BCF的法向量
与平面BCF的法向量![]() 的夹角,然后求其余角]
的夹角,然后求其余角]
(Ⅲ)由题意可知△ACF是等边三角形,设点N是△ACF的中心,
则点N一定在OF上,且|FN|=2|NO|,
在平面EOF内,作![]() OF,且
OF,且![]() 与EF交于M点.
与EF交于M点.
∵AC⊥OE,AC⊥OF,∴![]() 平面
平面![]() ,又
,又![]() 平面ACF.
平面ACF.
∴平面ACF⊥平面![]() ,又
,又![]() OF,∴
OF,∴![]() 平面ACF.∴三棱锥M-ACF是正三棱锥.
平面ACF.∴三棱锥M-ACF是正三棱锥.
在平面![]() 中,由
中,由![]() .
.
可知MN∥EO,又|FN|=2|NO|,∴|FM|=2|ME|.
在EF上存在一点M,使三棱锥M-ACF是正三棱锥,且点M是线段EF的靠近E的三等分点
[另法提示:本大题可将所给几何体补成正方体来进行求解]

 如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.
如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a. 如图,已知ABCD是底角为30°的等腰梯形,AD=2
如图,已知ABCD是底角为30°的等腰梯形,AD=2 如图,已知ABCD是边长为1的正方形,AF⊥平面ABCD,CE∥AF,CE=λAF(λ>1).
如图,已知ABCD是边长为1的正方形,AF⊥平面ABCD,CE∥AF,CE=λAF(λ>1). 如图,已知ABCD是矩形,PD⊥平面ABCD,PB=2,PB与平面ABCD所成的角为30°,PB与平面PCD所成的角为45°,求:
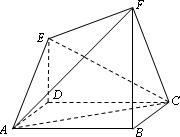
如图,已知ABCD是矩形,PD⊥平面ABCD,PB=2,PB与平面ABCD所成的角为30°,PB与平面PCD所成的角为45°,求: 如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.
如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.