题目内容
已知sinθ+cosθ=
解法一:∵sinθ+cosθ=![]() ,
,
两边平方得1+2sinθcosθ=![]() ,
,
∴2sinθcosθ=-![]() .
.
∵θ∈(0,π),∴cosθ<0<sinθ.
由(sinθ-cosθ)2=1-2sinθcosθ=![]() ,
,
得sinθ-cosθ=![]() .
.
将其与sinθ+cosθ=![]() 联立方程组,
联立方程组,
得sinθ=![]() ,cosθ=-
,cosθ=-![]() .
.
∴cotθ=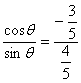 =-
=-![]() .
.
解法二:∵θ∈(0,π),sinθ+cosθ=![]() <1,
<1,
∴θ∈(![]() ,π),cosθ<0.
,π),cosθ<0.
依题意和基本三角恒等式,得方程组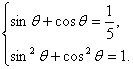
消去sinθ,得25cos2θ-5cosθ-12=0,
解得cosθ=-![]() 或cosθ=
或cosθ=![]() >0(舍去).
>0(舍去).
∴sinθ=![]() -cosθ=
-cosθ=![]() -(-
-(-![]() )=
)=![]() ,
,
cotθ=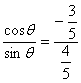 =-
=-![]() .
.

练习册系列答案
相关题目