题目内容
公比不是1的等比数列{an}的通项公式an=cosnβ,且对任意的n∈N*都有an+2=an,则该数列的前2009项的积为
______.
由an+2=anq2=an,
得到q2=1,又q≠1,所以q=-1,
令n=1,得到a1=cosβ,n=2时,a2=cos2β,
则
=
=q=-1,
化简得:2cos2β+cosβ-1=0,
即(2cosβ-1)(cosβ+1)=0,
解得cosβ=
或cosβ=-1,
所以此数列前2009项分别为-1,1,-1,…,-1或
,-
,
,…,-
,
则该数列的前2009项的积为-1或-
.
故答案为:-1或-
得到q2=1,又q≠1,所以q=-1,
令n=1,得到a1=cosβ,n=2时,a2=cos2β,
则
| a2 |
| a1 |
| 2cos2β -1 |
| cosβ |
化简得:2cos2β+cosβ-1=0,
即(2cosβ-1)(cosβ+1)=0,
解得cosβ=
| 1 |
| 2 |
所以此数列前2009项分别为-1,1,-1,…,-1或
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则该数列的前2009项的积为-1或-
| 1 |
| 22009 |
故答案为:-1或-
| 1 |
| 22009 |

练习册系列答案
相关题目
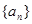 ,
,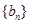 均为公比不是1的等比数列,设
均为公比不是1的等比数列,设 (
( ),那么数列
),那么数列