题目内容
若数列{an},{bn}均为公比不是1的等比数列,设cn=an+bn(n∈N*),那么数列{cn}( )
分析:依题意,对数列{an},{bn}的公比q(≠1)进行分类讨论,利用排除法进行判断即可.
解答:解:如果数列{an},{bn}的公比不相同时,数列{cn}一定不是等比数列,可排除A;
如果{an},{bn}的公比均为q(q≠1),则an+bn=(an-1+bn-1)q(n≥2),显然{cn}仍为等比数列,可排除B;
如果{an},{bn}的公比均为q(q≠1),且a1=-b1,则cn=0,故此时数列{cn}为等差数列,可排除D;
综上所述,数列{cn}有可能是等比数列,也有可能不是等比数列,即C正确.
故选C.
如果{an},{bn}的公比均为q(q≠1),则an+bn=(an-1+bn-1)q(n≥2),显然{cn}仍为等比数列,可排除B;
如果{an},{bn}的公比均为q(q≠1),且a1=-b1,则cn=0,故此时数列{cn}为等差数列,可排除D;
综上所述,数列{cn}有可能是等比数列,也有可能不是等比数列,即C正确.
故选C.
点评:本题考查等比关系的确定,考查举例说明与分类讨论思想,考查排除法在解答选择题中的应用,属于中档题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
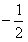 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;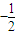 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;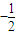 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;