题目内容
已知外接圆半径为6的△ABC的边长a、b、c,角B、C和面积S满足条件:S=a2-(b-c)2和 .
.
(1)求sinA的值;
(2)求△ABC面积的最大值.
解:(1)由S= bcsinA=2bc-(b2+c2-a2)=2bc-2bccosA得,
bcsinA=2bc-(b2+c2-a2)=2bc-2bccosA得, =
= =tan
=tan ,
,
∴ .
.
(2)(2)∵sinB+sinC= ,∴
,∴ +
+ =
= ,即b+c=
,即b+c= •2R=16,所以S=
•2R=16,所以S= bcsinA=
bcsinA=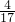 bc≤
bc≤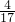 (
(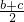 )2=
)2= ,
,
故当b=c=8时,△ABC面积取得最大值为 .
.
分析:(1)由三角形的面积公式,结合余弦定理求出tan 的值,进而有sinA=
的值,进而有sinA=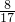 .
.
(2)利用sinB+sinC= ,结合正弦定理,求出b+c的值,利用三角形的面积公式和基本不等式求出面积的最大值.
,结合正弦定理,求出b+c的值,利用三角形的面积公式和基本不等式求出面积的最大值.
点评:本题是中档题,考查三角函数的化简,正弦定理、余弦定理的应用,三角形的面积公式以及基本不等式的应用,考查计算能力,逻辑推理能力,属于中档题.
 bcsinA=2bc-(b2+c2-a2)=2bc-2bccosA得,
bcsinA=2bc-(b2+c2-a2)=2bc-2bccosA得, =
= =tan
=tan ,
,∴
 .
.(2)(2)∵sinB+sinC=
 ,∴
,∴ +
+ =
= ,即b+c=
,即b+c= •2R=16,所以S=
•2R=16,所以S= bcsinA=
bcsinA=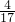 bc≤
bc≤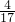 (
(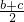 )2=
)2= ,
,故当b=c=8时,△ABC面积取得最大值为
 .
.分析:(1)由三角形的面积公式,结合余弦定理求出tan
 的值,进而有sinA=
的值,进而有sinA=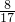 .
.(2)利用sinB+sinC=
 ,结合正弦定理,求出b+c的值,利用三角形的面积公式和基本不等式求出面积的最大值.
,结合正弦定理,求出b+c的值,利用三角形的面积公式和基本不等式求出面积的最大值.点评:本题是中档题,考查三角函数的化简,正弦定理、余弦定理的应用,三角形的面积公式以及基本不等式的应用,考查计算能力,逻辑推理能力,属于中档题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 .
. (a,b,c为角A,B,C所对的边)
(a,b,c为角A,B,C所对的边)