题目内容
已知椭圆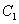 :
: 的右顶点为
的右顶点为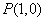 ,过
,过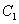 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为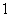 .
.
(I)求椭圆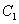 的方程;
的方程;
(II)设抛物线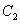 :
: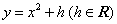 的焦点为F,过F点的直线
的焦点为F,过F点的直线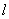 交抛物线与A、B两点,过A、B两点分别作抛物线
交抛物线与A、B两点,过A、B两点分别作抛物线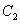 的切线交于Q点,且Q点在椭圆
的切线交于Q点,且Q点在椭圆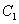 上,求
上,求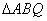 面积的最值,并求出取得最值时的抛物线
面积的最值,并求出取得最值时的抛物线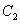 的方程。
的方程。
解:(I)由题意得 所求的椭圆方程为
所求的椭圆方程为
(II)令
设切线AQ方程为 代入
代入 令
令 可得
可得
抛物线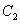 在点A处的切线斜率为
在点A处的切线斜率为
所以切线AQ方程为: 
同理可得BQ方程为: 
联立
 解得Q点为
解得Q点为
焦点F坐标为(0,  ), 令l方程为:
), 令l方程为:  代入
代入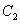 :
:
得:  由韦达定理有:
由韦达定理有:
所以Q点为
过Q作y轴平行线交AB于M点, 则
M点为 ,
,
 ,
, 
 -而Q点在椭圆上,
-而Q点在椭圆上, 



练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 实数,且y=x}, 则A ∩ B的子集个数为_______.
实数,且y=x}, 则A ∩ B的子集个数为_______. 所得弦长为2,则圆心C的轨迹方程为 .
所得弦长为2,则圆心C的轨迹方程为 . 、
、 分别为具有公共焦点
分别为具有公共焦点 、
、 的椭圆和双曲线的离心率,
的椭圆和双曲线的离心率, 是两曲线的一个公共点,且满足
是两曲线的一个公共点,且满足 ,则
,则 的值为
的值为 B.2 C.
B.2 C. D.1
D.1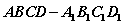 ,
,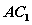 与平面
与平面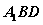 ,
,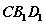 交于
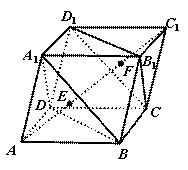
交于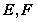 两点。给出以下命题,其中真命题有______(写出所有正确命题的序号)
两点。给出以下命题,其中真命题有______(写出所有正确命题的序号)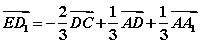 ;
;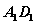 中点为
中点为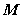 ,
,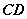 的中点为
的中点为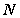 ,则直线
,则直线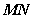 与面
与面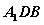 有一个交点;
有一个交点;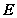 为
为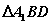 的内心;
的内心;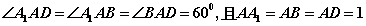 ,则三棱锥
,则三棱锥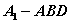 为正三棱锥,且
为正三棱锥,且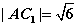 .
.
 为等差数列,其前
为等差数列,其前 项和为
项和为 .若
.若 ,
, ,
, ,则
,则 .
. 是双曲线
是双曲线 的两个焦点,
的两个焦点, 是
是 上一点,若
上一点,若 ,且
,且 的最小内角为
的最小内角为 ,则
,则 =a,
=a, b,
b, =c,则
=c,则 =( )
=( )
 在一个周期内的图象,此函数的解析式为可为( )
在一个周期内的图象,此函数的解析式为可为( ) B.
B.
 ) D.
) D.
