题目内容
设集合 为函数
为函数 的定义域,集合
的定义域,集合 为函数
为函数 的值域,集合
的值域,集合 为不等式
为不等式 的解集.
的解集.
(1)求 ;
;
(2)若 ,求
,求 的取值范围.
的取值范围.
(1)
 .(2)
.(2) .
.
解析试题分析:(1)通过确定函数的定义域、值域得到集合 ,进一步确定
,进一步确定 .本题较为简单,突出对函数的定义域、值域的确定方法,集合的运算等,进行考查.
.本题较为简单,突出对函数的定义域、值域的确定方法,集合的运算等,进行考查.
(2)通过解不等式 ,得到集合
,得到集合 ,并进一步确定
,并进一步确定 ,利用
,利用
得到 的不等式.注意讨论
的不等式.注意讨论 的不同取值范围,得到不等式解集的不同形式.
的不同取值范围,得到不等式解集的不同形式.
试题解析:(1)由 ,解得
,解得 又
又 ,
,
所以, .所以,
.所以,
 .
.
(2)因为 ,由
,由 ,知
,知 .
.
①当a>0时,由 ,得C=
,得C= ,不满足
,不满足 ;
;
②当a<0时,由 ,得
,得 ,
,
欲使 ,则
,则 ,解得
,解得 或
或 .又a<0,所以
.又a<0,所以 .
.
综上所述,所求 的取值范围是
的取值范围是 .
.
考点:函数的定义域、值域,集合的运算,一元二次不等式解法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, 
 ,请用列举法表示集合B;
,请用列举法表示集合B; 和
和 .
.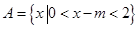 ,
,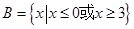 .分别求出满足下列条件的实数
.分别求出满足下列条件的实数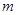 的取值范围.
的取值范围.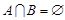 ;
;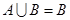 .
. },B={x|y=ln(1-2x)}.
},B={x|y=ln(1-2x)}. ,
,
 ,
, .
. ;(2)如果集合
;(2)如果集合 ,写出
,写出 的所有真子集.
的所有真子集. 为函数
为函数 的定义域,集合
的定义域,集合 .
. ;
; 的取值范围.
的取值范围. 的定义域为集合
的定义域为集合 ,函数
,函数 的定义域为集合
的定义域为集合 .
. ;
; ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围. ,
, ,且
,且 ,求实数
,求实数 的取值范围。
的取值范围。
 的定义域为集合A,函数
的定义域为集合A,函数
 的定义域为集合B
的定义域为集合B 时,求
时,求
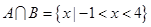 ,求实数
,求实数 的值
的值