题目内容
已知二次函数 满足
满足 且
且 的图像在
的图像在 处的切线垂直于直线
处的切线垂直于直线 .
.
(1)求 的值;
的值;
(2)若方程 有实数解,求
有实数解,求 的取值范围.
的取值范围.
【答案】
(1)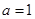 ,
,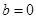 ;(2)
;(2)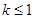 .
.
【解析】
试题分析:本题考查导数的应用、分段函数值域以及函数图像等基础知识,考查转化的思想方法,考查综合运用数学知识分析问题解决问题的能力.第一问,考查求切线方程的解题过程,因为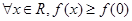 ,所以
,所以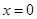 是对称轴,所以
是对称轴,所以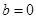 ,再利用两直线的垂直关系列出斜率表达式,解出
,再利用两直线的垂直关系列出斜率表达式,解出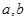 ;第二问,将方程根的问题转化成求函数最值问题,再利用数形结合法解题.
;第二问,将方程根的问题转化成求函数最值问题,再利用数形结合法解题.
试题解析: (1)∵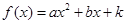 满足
满足 ,∴
,∴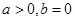 ,
,
又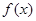 的图象在
的图象在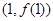 处的切线垂直于
处的切线垂直于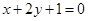
∴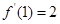 ,即
,即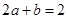 ∴
∴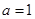 ,
,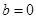 , ∴
, ∴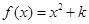
(2)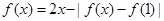 有实数解转化为
有实数解转化为
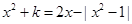 即
即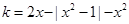 有实数解,
有实数解,
当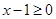 即
即 或
或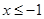 时
时 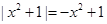 ;
;
当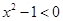 即
即 时
时  ,
,
原问题等价于求函数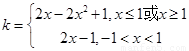 的值域,
的值域,
易知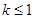 ,
,
∴方程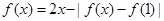 有实数解时
有实数解时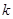 的取值范围是
的取值范围是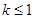 .
.
考点:1.用导数求切线方程;2.求分段函数值域.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 , 满足
, 满足 且
且 的最小值是
的最小值是 .(Ⅰ)求
.(Ⅰ)求 ,若函数
,若函数 在区间
在区间 上是单调函数,求实数
上是单调函数,求实数 的取值范围。
的取值范围。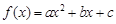 , 满足
, 满足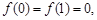 且
且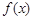 的最小值是
的最小值是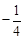 .
.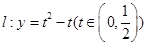 ,若直线
,若直线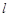 与
与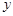 轴所围成封闭图形的面积是
轴所围成封闭图形的面积是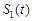 , 直线
, 直线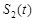 ,设
,设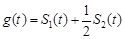 ,当
,当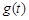 取最小值时,求
取最小值时,求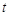 的值.
的值.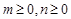 , 求证:
, 求证: 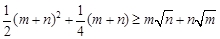 .
.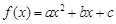 , 满足
, 满足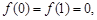 且
且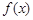 的最小值是
的最小值是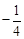 .
.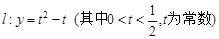 ,若直线
,若直线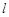 与
与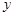 轴这二条直线和一条曲线所围成封闭图形的面积是
轴这二条直线和一条曲线所围成封闭图形的面积是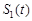 , 直线
, 直线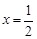 这二条直线和一条曲线所围成封闭图形的面积是
这二条直线和一条曲线所围成封闭图形的面积是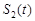 ,已知
,已知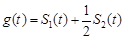 ,当
,当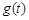 取最小值时,求
取最小值时,求 的值.
的值.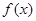 满足
满足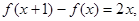 且
且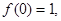
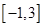 上,
上,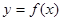 的图像恒在
的图像恒在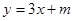 的图像的上方。求实数m的取值范围。
的图像的上方。求实数m的取值范围。