题目内容
已知二次函数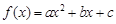 , 满足
, 满足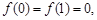 且
且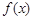 的最小值是
的最小值是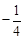 .
.
(1) 求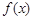 的解析式;
的解析式;
(2) 设直线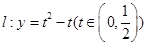 ,若直线
,若直线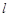 与
与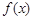 的图象以及
的图象以及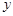 轴所围成封闭图形的面积是
轴所围成封闭图形的面积是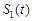 , 直线
, 直线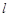 与
与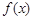 的图象所围成封闭图形的面积是
的图象所围成封闭图形的面积是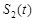 ,设
,设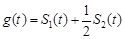 ,当
,当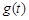 取最小值时,求
取最小值时,求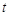 的值.
的值.
(3)已知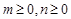 , 求证:
, 求证: 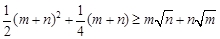 .
.
【答案】
(1) 
(2) 
(3)证明略
【解析】(1)由二次函数图象的对称性, 可设 ,又
,又
故 …………………3分
…………………3分
(2) 据题意,
直线 与
与 的图象的交点坐标为
的图象的交点坐标为 和
和 ,由定积分的几何意
,由定积分的几何意
义知 ……5分
……5分
=

= …………………7分
…………………7分
而
令 或
或 (不合题意,舍去)
(不合题意,舍去)
当  …………………8分
…………………8分
故当 时,
时, 有最小值. ………………………………………………9分
有最小值. ………………………………………………9分
(3)  的最小值为
的最小值为
 ……①
……① ……②
…………………………………………10分
……②
…………………………………………10分
由①+②得: 
 ………③
…………………11分
………③
…………………11分
又
 ④
…………………12分
④
…………………12分
故
 ……13分
……13分

练习册系列答案
相关题目
 满足f(1+x)=f(1-x)且方程
满足f(1+x)=f(1-x)且方程 有等根
有等根 满足条件
满足条件 ,及
,及 .
. 上的最大和最小值.
上的最大和最小值. 满足
满足 ,且关于
,且关于 的方程
的方程 的两实数根分别在区间(-3,-2),(0,1)内。
的两实数根分别在区间(-3,-2),(0,1)内。 的取值范围;
的取值范围; 在区间(-1-
在区间(-1- ,1-
,1- 满足
满足 且
且 .
. 上,
上,  的图象上方,试确定实数
的图象上方,试确定实数 的范围.
的范围.