题目内容
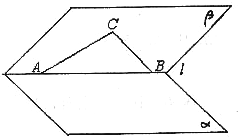 如图已知:平面α与平面β所成角为60°,直角三角形斜边AB在棱l上,直角边BC,CA在平面β内,它们与平面α所成角分别为θ1,θ2.
如图已知:平面α与平面β所成角为60°,直角三角形斜边AB在棱l上,直角边BC,CA在平面β内,它们与平面α所成角分别为θ1,θ2.求:sin2θ1+sin2θ2的值.
分析:过点C作平面α的垂线,垂足为O,则∠CBO=θ1,∠CAO=θ2,过O作l的垂线,垂足为G,则∠CGO=60°为二面角α-l-β的平面角,再分别表示出θ1,θ2与∠CGO的正弦值,并且结合直角三角形的性质得到答案.
解答:解:过点C作平面α的垂线,垂足为O,则∠CBO=θ1,∠CAO=θ2,
过O作l的垂线,垂足为G,则∠CGO=60°为二面角α-l-β的平面角,
所以sinθ1=
,sinθ2=
,sin60°=
,
所以sin2θ1+sin2θ2=
=
=
=
=sin260°=
.
过O作l的垂线,垂足为G,则∠CGO=60°为二面角α-l-β的平面角,
所以sinθ1=
| OC |
| BC |
| OC |
| AC |
| OC |
| GC |
所以sin2θ1+sin2θ2=
| OC2•(AC2+BC2) |
| AC2•BC2 |
| OC2•AB2 |
| AC2•BC2 |
| OC2•AB2 |
| GC2•AB2 |
| OC2 |
| GC2 |
| 3 |
| 4 |
点评:解决此类问题的关键是熟练掌握线面角与二面角平面角的定义与作法,以及直角三角形的有关性质,此题综合性较强属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
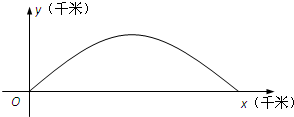 (2012•江苏)如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-
(2012•江苏)如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-


 ,
,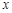 轴在地平面上,
轴在地平面上,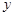 轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程
轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程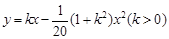 表示的曲线上,其中
表示的曲线上,其中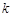 与发射方向有关.炮的射程是指炮弹落地点的横坐标.
与发射方向有关.炮的射程是指炮弹落地点的横坐标.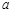 不超过多少时,炮弹可以击中它?请说明理由.
不超过多少时,炮弹可以击中它?请说明理由.