题目内容
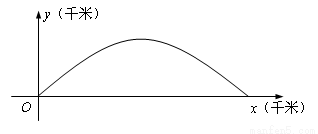
如图2,建立平面直角坐标系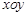 ,
,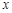 轴在地平面上,
轴在地平面上,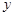 轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程
轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程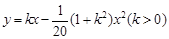 表示的曲线上,其中
表示的曲线上,其中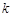 与发射方向有关.炮的射程是指炮弹落地点的横坐标.
与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标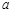 不超过多少时,炮弹可以击中它?请说明理由.
不超过多少时,炮弹可以击中它?请说明理由.
【答案】
(1)10 km(2)见解析
【解析】解:(1)令y=0,得kx-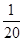 (1+k2)x2=0,…………………………2分
(1+k2)x2=0,…………………………2分
由实际意义和题设条件知x>0,k>0,
故x= =
=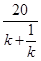 ≤
≤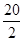 =10,当且仅当k=1时取等号. …………………………4分
=10,当且仅当k=1时取等号. …………………………4分
所以炮的最大射程为10 km. …………………5分
(2)因为a>0,所以炮弹可击中目标⇔存在k>0,使3.2=ka-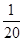 (1+k2)a2成立
(1+k2)a2成立
⇔关于k的方程a2k2-20ak+a2+64=0有正根 …………………………7分
⇔判别式Δ=(-20a)2-4a2(a2+64)≥0
⇔a≤6. ………………11分
所以当a不超过6 km时,可击中目标. ……………………12分

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 已知矩形ABCD中,
已知矩形ABCD中,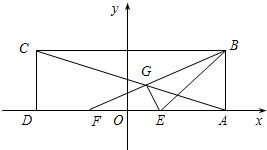 在矩形ABCD中,已知AD=6,AB=2,E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为⊙H.以DA所在直线为x轴,以DA中点O为坐标原点,建立如图所示的平面直角坐标系.
在矩形ABCD中,已知AD=6,AB=2,E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为⊙H.以DA所在直线为x轴,以DA中点O为坐标原点,建立如图所示的平面直角坐标系. 已知长方形ABCD,AB=
已知长方形ABCD,AB= (2013•日照一模)已知长方形EFCD,
(2013•日照一模)已知长方形EFCD,