题目内容
已知函数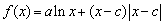 ,
,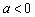 ,
,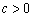 .
.
(1)当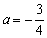 ,
,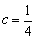 时,求函数
时,求函数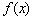 的单调区间;
的单调区间;
(2)当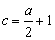 时,若
时,若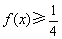 对
对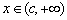 恒成立,求实数
恒成立,求实数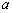 的取值范围;
的取值范围;
(3)设函数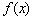 的图象在点
的图象在点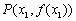 、
、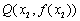 两处的切线分别为
两处的切线分别为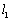 、
、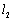 .若
.若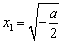 ,
,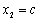 ,且
,且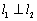 ,求实数
,求实数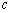 的最小值.
的最小值.
解:函数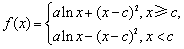 ,求导得
,求导得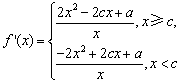 .
.
(1)当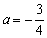 ,
,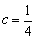 时,
时,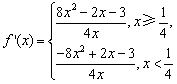 ,
,
若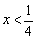 ,则
,则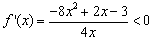 恒成立,
恒成立, 所以
所以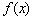 在
在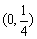 上单调减;
上单调减;
若 ,则
,则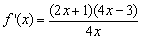 ,令
,令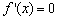 ,解得
,解得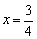 或
或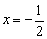 (舍),
(舍),
当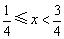 时,
时,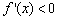 ,
,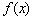 在
在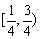 上单调减;
上单调减;
当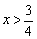 时,
时,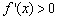 ,
,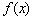 在
在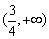 上单调增.
上单调增.
所以函数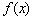 的单调减区间是
的单调减区间是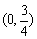 ,单调增区间是
,单调增区间是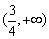 . ………………4分
. ………………4分
(2)当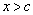 ,
,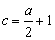 时,
时,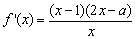 ,而
,而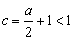 ,所以
,所以
当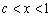 时,
时,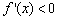 ,
,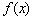 在
在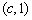 上单调减;
上单调减;
当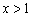 时,
时,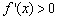 ,
,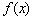 在
在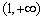 上单调增.
上单调增.
所以函数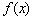 在
在 上的最小值为
上的最小值为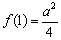 ,
,
所以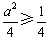 恒成立,解得
恒成立,解得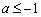 或
或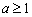 ,
,
又由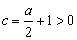 ,得
,得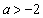 ,所以实数
,所以实数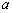 的取值范围是
的取值范围是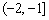 . ……………9分
. ……………9分
(3)由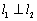 知,
知,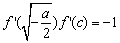 ,而
,而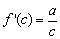 ,则
,则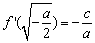 ,
,
若 ,则
,则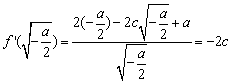 ,所以
,所以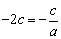 ,
,
解得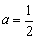 ,不符合题意; ……………………………11分
,不符合题意; ……………………………11分
故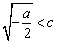 ,则
,则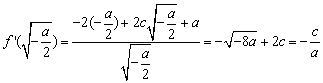 ,
,
整理得,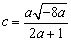 ,由
,由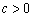 得,
得,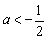 , …………………………13分
, …………………………13分
令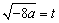 ,则
,则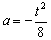 ,
,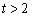 ,所以
,所以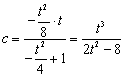 ,
,
设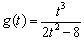 ,则
,则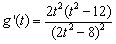 ,
,
当 时,
时,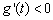 ,
,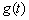 在
在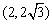 上单调减;
上单调减;
当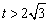 时,
时, ,
,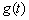 在
在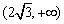 上单调增.
上单调增.
所以,函数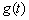 的最小值为
的最小值为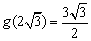 ,故实数
,故实数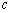 的最小值为
的最小值为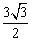 . ……16分
. ……16分

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
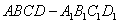 为棱长为1,动点
为棱长为1,动点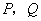 分别在棱
分别在棱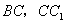 上,过点
上,过点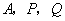 的平面截该正方体所得的截面记为
的平面截该正方体所得的截面记为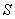 ,设
,设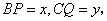 其中
其中 ,下列命题正确的是
,下列命题正确的是  时,
时,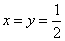 时,
时,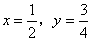 时,
时,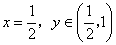 时,设
时,设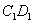 的交点为
的交点为 ,则
,则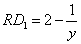
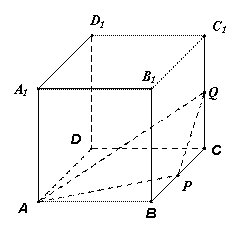
 ,则不等式
,则不等式 的解集是 .
的解集是 . 中,内角
中,内角 ,
, ,
, 的对
的对 边分别为
边分别为 ,
, ,
, ,且
,且 .
. ,求
,求 的面积的最大值.
的面积的最大值.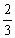 ,游览户部山、子房山和九里山的概率都是
,游览户部山、子房山和九里山的概率都是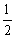 ,且该游客是否游览这四座山相互独立.
,且该游客是否游览这四座山相互独立.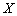 表示
表示 .
. 的图象大致为
的图象大致为
 ,以下说法正确的是( )
,以下说法正确的是( ) ,
, ,则
,则 ,
, ,
, ,则
,则 ,
, 则
则 ( )
( ) (B) 2011
(B) 2011