题目内容
已知![]() 。
。
(1)求函数![]() 的最小值;
的最小值;
(2)若存在![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)证明对一切![]() ,都有
,都有![]() 成立。
成立。
解:(1)![]() 的定义域为
的定义域为![]() ,
,![]() , ……………1分
, ……………1分
令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() , ……………3分
, ……………3分
所以![]() 在
在![]() 上单调递减;在
上单调递减;在![]() 上单调递增,
上单调递增,
故当![]() 时
时![]() 取最小值为
取最小值为![]() 。 ……………5分
。 ……………5分
(2)存在![]() ,使
,使![]() 成立,即
成立,即![]() 在
在![]() 能成立,等价于
能成立,等价于![]() 在
在![]() 能成立;
能成立;
等价于![]() ……………8分
……………8分
记![]() ,
,![]()
则![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以当![]() 时
时![]() 取最小值为4,故
取最小值为4,故![]() 。 ……………11分
。 ……………11分
(3)记![]()
![]() ,则
,则![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以当![]() 时
时![]() 取最大值为
取最大值为![]() 。 ……………14分
。 ……………14分
又由(1)知当![]() 时
时![]() 取最小值为
取最小值为![]() ,
,
故对一切![]() ,都有
,都有![]() 成立。 ……………16分
成立。 ……………16分

练习册系列答案
相关题目
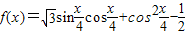 .
.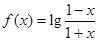 .
.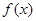 的定义域;
的定义域;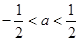 ,试比较
,试比较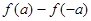 与
与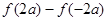 的大小.
的大小.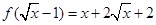 ,
,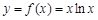 .
.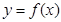 的图像在
的图像在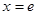 处的切线方程;
处的切线方程;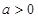 ,求函数
,求函数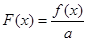 在
在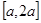 上的最大值;
上的最大值;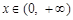 ,都有
,都有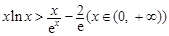 成立。
成立。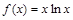 .
. 在区间
在区间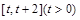 上的最小值;
上的最小值;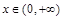 ,
, 恒成立,求实数
恒成立,求实数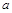 的取值范围;
的取值范围;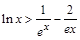 恒成立.
恒成立.