题目内容
20.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-4x+4,x>0}\\{0,x=0}\\{{x}^{2}+4x+4,x<0}\end{array}\right.$(Ⅰ)求f(1),f(-3),f(a+1)的值;
(Ⅱ)求函数f(x)的零点.
分析 (Ⅰ)直接利用分段函数求f(1),f(-3),f(a+1)的值;
(Ⅱ)利用分段函数,通过分类讨论列出方程求解函数f(x)的零点.
解答 (本小题满分12分)
解:(Ⅰ)因为1>0,所以f(1)=12-4×1+4=1; (1分)
因为-3<0,所以f(-3)=(-3)2+4×(-3)+4=1; (2分)
当a+1>0,即a>-1时,f(a+1)=(a+1)2-4(a+1)+4=a2-2a+1; (3分)
当a+1=0,即a=-1时,f(a+1)=0; (4分)
当a+1<0,即a<-1时,f(a+1)=(a+1)2+4(a+1)+4=a2+6a+9; (5分)
所以$f(a+1)=\left\{\begin{array}{l}{a^2}-2a+1,a>-1\\ 0,a=-1\\{a^2}+6a+9,a<-1.\end{array}\right.$(6分)
(Ⅱ)由题意,得$\left\{\begin{array}{l}x>0\\{x^2}-4x+4=0\end{array}\right.$,解得x=2; (8分)
或$\left\{\begin{array}{l}x<0\\{x^2}+4x+4=0\end{array}\right.$,解得x=-2.(10分)
又因为f(0)=0,(11分)
所以函数f(x)的零点为2、0与-2.(12分)
点评 本题考查分段函数的应用,分类讨论思想以及函数思想的应用,考查计算能力.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
10.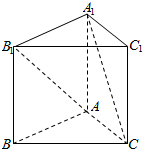 如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,则异面直线AB1和A1C所成的角的余弦值大小为( )
如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,则异面直线AB1和A1C所成的角的余弦值大小为( )
 如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,则异面直线AB1和A1C所成的角的余弦值大小为( )
如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,则异面直线AB1和A1C所成的角的余弦值大小为( )| A. | $\frac{1}{4}$ | B. | $-\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
8.已知向量$\overrightarrow{a}$=(-1,0),$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
15.若连续抛掷两次骰子得到的点数分别为m,n,则点P(m,n)在函数y=-x+4图象上的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
5.“x<1”是“|x|<2”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
12.设α,β是两个不同的平面,直线m⊥α,则“m⊥β”是“α∥β”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |