题目内容
已知函数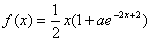 .
.
(Ⅰ)若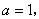 记
记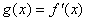 ,求证:当
,求证:当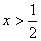 时,
时, ;
;
(Ⅱ)若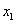 ,
, 是函数
是函数 的两个极值点,且
的两个极值点,且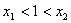 ,若
,若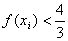 (
(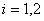 ),求实数
),求实数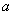 的取值范围.(注:
的取值范围.(注: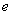 是自然对数的底数.)
是自然对数的底数.)
解(Ⅰ) 因为 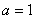 ,所以
,所以 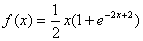
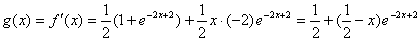
由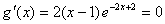 得
得 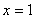
当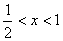 时,
时,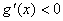 ,
,
当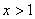 时,
时,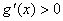
所以,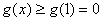
又因为 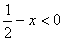 ,所以,
,所以,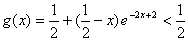
所以,当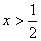 时,
时,
(Ⅱ) 由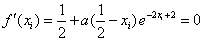 得:
得: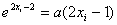
因为方程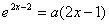 有两解,所以
有两解,所以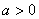
由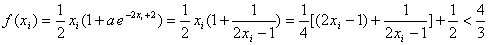
解得: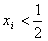 或
或 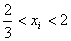
(ⅰ) 当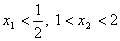 时,
时, 
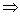 无解
无解
(ⅱ) 当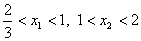 时,
时, 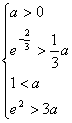 解得
解得 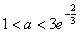
所以,实数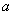 的取值范围为
的取值范围为 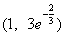

练习册系列答案
相关题目
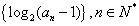 为等差数列,且
为等差数列,且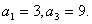
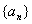 的通项公式;
的通项公式; 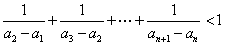 。
。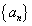 满足
满足 ,且
,且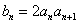 ,则数列
,则数列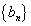 的前50项和为______|
的前50项和为______|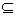 M={1,2,3,…,11},把满足以下条件:若
M={1,2,3,…,11},把满足以下条件:若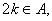 则
则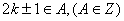 的集合A称为好集,则含有至少3个偶数的好集合的个数为 ( )
的集合A称为好集,则含有至少3个偶数的好集合的个数为 ( )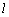 与曲线
与曲线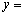 e
e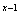 交于不同的A,B两点,分别过点A,B作
交于不同的A,B两点,分别过点A,B作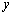 轴的平行线,与曲线
轴的平行线,与曲线 交于点C,D,则直线CD的斜率是 .
交于点C,D,则直线CD的斜率是 .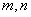 为异面直线,
为异面直线,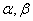 为两个不同平面,
为两个不同平面,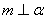 ,
,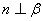 ,且直线
,且直线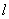 满足
满足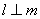 ,
,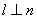 ,
,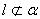 ,
,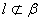 ,则( )
,则( )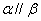 且
且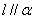 B.
B.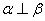 且
且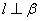
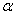 与
与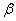 相交,且交线垂直于
相交,且交线垂直于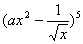 的展开式中各项系数的和为243,则该展开式中的常数项的值为_____________.
的展开式中各项系数的和为243,则该展开式中的常数项的值为_____________. ”,应假设为( ).
”,应假设为( ). C.
C. D.
D.
 的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,它落在阴影区域内的概率是
的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,它落在阴影区域内的概率是 ,则阴影部分的面积是( )
,则阴影部分的面积是( ) .
. .
.
 .
.
 .
.
