题目内容
 13、如图所示,已知AP是圆O的切线,P为切点,AC是圆O的割线,与圆O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.则∠OAM+∠APM的大小为
13、如图所示,已知AP是圆O的切线,P为切点,AC是圆O的割线,与圆O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.则∠OAM+∠APM的大小为90°
.分析:由题意及图知APOM四点共圆,故可证得∠OAM=∠OPM,则∠OAM+∠APM=∠OPM+∠APM易得两角和为90°
解答:解:如图,连接OP,OM,由题意知OP⊥AP,OM⊥AM,故有∠APO+∠AM0=π,可得四边形AMOP四点共圆
∵∠OAM,∠OPM是同弦OM所对的角,
∴∠OAM=∠OPM
∴∠OAM+∠APM=∠OPM+∠APM=90°
故答案为:90°.
∵∠OAM,∠OPM是同弦OM所对的角,
∴∠OAM=∠OPM
∴∠OAM+∠APM=∠OPM+∠APM=90°
故答案为:90°.
点评:本题考查弦切角,正确解答本题,关键是由题设条件证明出四边形AMOP四点共圆从而将求∠OAM+∠APM的大小问题变为∠OPM+∠APM=90°的问题,使问题简化,本题中灵活转化,使得解题难度大大降低,做题时应该注意转化一下看问题的角度,思路就会开阔了.

练习册系列答案
相关题目
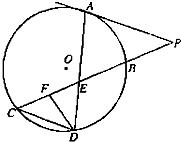 如图所示,已知PA是⊙O相切,A为切点,PBC为割线,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.
如图所示,已知PA是⊙O相切,A为切点,PBC为割线,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF•EC.

 如图所示,已知AP是圆O的切线,P为切点,AC是圆O的割线,与圆O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.则∠OAM+∠APM的大小为________.
如图所示,已知AP是圆O的切线,P为切点,AC是圆O的割线,与圆O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.则∠OAM+∠APM的大小为________.