题目内容
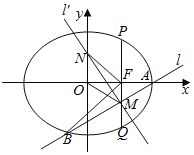
【题目】已知椭圆![]() 的上下两个焦点分别为
的上下两个焦点分别为![]() ,过点
,过点![]() 与
与![]() 轴垂直的直线交椭圆
轴垂直的直线交椭圆![]() 于
于![]() 两点,
两点,![]() 的面积为
的面积为![]() ,椭圆
,椭圆![]() 的长轴长是短轴长的
的长轴长是短轴长的![]() 倍.
倍.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() 为坐标原点,直线
为坐标原点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭园
,与椭园![]() 交于
交于![]() 两个不同的点,若存在实数
两个不同的点,若存在实数![]() ,使得
,使得![]() ,求
,求![]() 的取值范围,
的取值范围,
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据已知设椭圆的焦距![]() ,当
,当![]() 时,
时,![]() ,由题意得,
,由题意得,![]() 的面积为
的面积为![]() ,
,![]() ,
,![]() ,解得
,解得![]() 即可;
即可;
(2)设![]() ,
,![]() ,
,![]() ,分类讨论:当
,分类讨论:当![]() 时,利用椭圆的对称性即可得出;
时,利用椭圆的对称性即可得出;![]() 时,直线
时,直线![]() 的方程与椭圆的方程联立得到
的方程与椭圆的方程联立得到![]() 及根与系数的关系,再利用向量相等,代入计算即可得出.
及根与系数的关系,再利用向量相等,代入计算即可得出.
(1)由题意可得![]() ,则
,则![]() ,则
,则![]() ,
,
![]()
![]() 的面积
的面积![]() , ①
, ①
![]() 椭圆
椭圆![]() 的长轴长是短轴长的
的长轴长是短轴长的![]() 倍,
倍,
![]()
![]() ②,
②,
![]()
![]() ③,
③,
由①②③解得![]() ,
,![]() ,
,
∴椭圆![]() 的标准方程
的标准方程![]() .
.
(2)当![]() 时,则
时,则![]() ,由椭圆的对称性得
,由椭圆的对称性得![]() ,即
,即![]()
![]()
![]() 时,存在实数
时,存在实数![]() ,使得
,使得![]() ,
,
当![]() 时,得
时,得![]() ,
,
![]()
![]() 三点共线,
三点共线,![]()
![]() ,
,
设![]() ,
,![]()
由![]() ,得(
,得(![]() ,
,
由已知得![]() ,即
,即![]()
且![]() ,
,![]() .
.
由![]() 得
得![]() ,
,
![]() ,
,
![]()
 , 显然
, 显然![]() 不成立,
不成立,
![]()
![]()
![]()
![]() ,
,
![]()
![]() ,即
,即![]() .
.
解得![]() 或
或![]() .
.
综上所述,![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
【题目】有一个同学家开了一个奶茶店,他为了研究气温对热奶茶销售杯数的影响,从一季度中随机选取5天,统计出气温与热奶茶销售杯数,如表:
气温 | 0 | 4 | 12 | 19 | 27 |
热奶茶销售杯数 | 150 | 132 | 130 | 104 | 94 |
(Ⅰ)求热奶茶销售杯数关于气温的线性回归方程![]() (
(![]() 精确到0.1),若某天的气温为15oC,预测这天热奶茶的销售杯数;
精确到0.1),若某天的气温为15oC,预测这天热奶茶的销售杯数;
(Ⅱ)从表中的5天中任取一天,若已知所选取该天的热奶茶销售杯数大于120,求所选取该天热奶茶销售杯数大于130的概率.
参考数据:![]() ,
,![]() .参考公式:
.参考公式: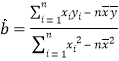 ,
,![]()