题目内容
如图为一半径为3m的水轮,水轮中心O距水面2m,已知水轮每分钟旋转4圈,水轮上的点P到水面距离y(m)与时间x(t)满足函数关系y=Asin(ωx+φ)+2则( )
A.ω=
 ,A=5
,A=5B.ω=
 ,A=5
,A=5C.ω=
 ,A=3
,A=3D.ω=
 ,A=3
,A=3
【答案】分析:根据题意,水轮旋转一周所用的时间为一个周期,由周期公式,T= 求解;A为最大振幅,由图象知到最高点时即为A值.
求解;A为最大振幅,由图象知到最高点时即为A值.
解答:解:已知水轮每分钟旋转4圈
∴ω=
又∵半径为3m,水轮中心O距水面2m,
∴最高点为5,即A=3,
故选D.
点评:本题主要通过一个实际背景来考查三角函数的周期及振幅.
 求解;A为最大振幅,由图象知到最高点时即为A值.
求解;A为最大振幅,由图象知到最高点时即为A值.解答:解:已知水轮每分钟旋转4圈
∴ω=

又∵半径为3m,水轮中心O距水面2m,
∴最高点为5,即A=3,
故选D.
点评:本题主要通过一个实际背景来考查三角函数的周期及振幅.

练习册系列答案
相关题目
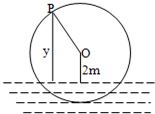 如图为一半径为3m的水轮,水轮中心O距水面2m,已知水轮每分钟旋转4圈,水轮上的点P到水面距离y(m)与时间x(t)满足函数关系y=Asin(ωx+φ)+2则( )
如图为一半径为3m的水轮,水轮中心O距水面2m,已知水轮每分钟旋转4圈,水轮上的点P到水面距离y(m)与时间x(t)满足函数关系y=Asin(ωx+φ)+2则( )A、ω=
| ||
B、ω=
| ||
C、ω=
| ||
D、ω=
|
 则(
)
则(
)
 B.
B. C.
C.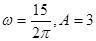 D.
D.


 ,A=5
,A=5 ,A=5
,A=5 ,A=3
,A=3 ,A=3
,A=3