题目内容
已知函数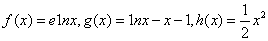 .
.
(1)求函数g(x)的极大值;
(2)求证:存在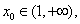 ,使
,使 ;
;
(3)对于函数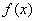 与h(x)定义域内的任意实数x,若存在常数k、b使得
与h(x)定义域内的任意实数x,若存在常数k、b使得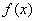 ≤kx +b和
≤kx +b和
h(x)≥kx+b都成立,则称直线y=kx+b为函数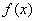 与h(x)的分界线,试探究函数
与h(x)的分界线,试探究函数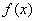 与h(x)是否存在“分界线”?若存在,请给予汪明,并求出k、b的值:若不存在,请说明理由。
与h(x)是否存在“分界线”?若存在,请给予汪明,并求出k、b的值:若不存在,请说明理由。
(1)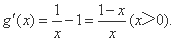
令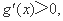 解得
解得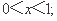
令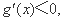 解得
解得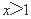 .
.
∴函数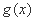 在(0,1)内单调递增,在
在(0,1)内单调递增,在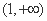 上单调递减.
上单调递减.
所以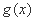 的极大值为
的极大值为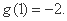
(2)由(Ⅰ)知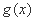 在(0,1)内单调递增,在
在(0,1)内单调递增,在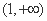 上单调递减,
上单调递减,
令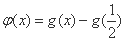
∴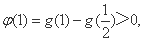
取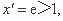 则
则

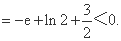
故存在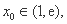 使
使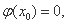 即存在
即存在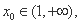 使
使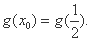
(说明: 的取法不唯一,只要满足
的取法不唯一,只要满足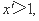 且
且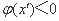 即可)
即可)
(3)设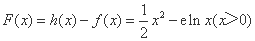
则
则当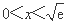 时,
时,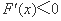 ,函数
,函数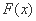 单调递减;
单调递减;
当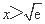 时,
时,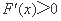 ,函数
,函数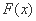 单调递增.
单调递增.
∴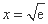 是函数
是函数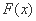 的极小值点,也是最小值点,
的极小值点,也是最小值点,
∴
∴函数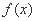 与
与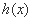 的图象在
的图象在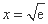 处有公共点(
处有公共点(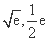 ).
).
设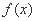 与
与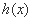 存在“分界线”且方程为
存在“分界线”且方程为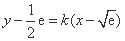 ,
,
令函数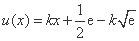
①由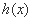 ≥
≥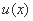 ,得
,得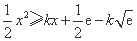 在
在 上恒成立,
上恒成立,
即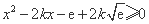 在
在 上恒成立,
上恒成立,
∴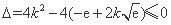 ,
,
即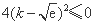 ,
,
∴ ,故
,故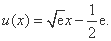
②下面说明: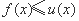 ,
,
即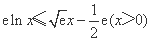 恒成立.
恒成立.
设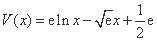
则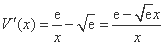
∵当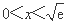 时,
时,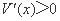 ,函数
,函数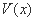 单调递增,
单调递增,
当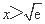 时,
时,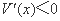 ,函数
,函数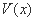 单调递减,
单调递减,
∴当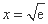 时,
时,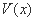 取得最大值0,
取得最大值0,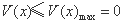 .
.
∴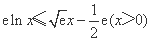 成立.
成立.
综合①②知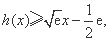 且
且
故函数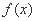 与
与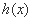 存在“分界线”
存在“分界线”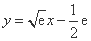 ,
,
此时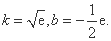 …
…

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
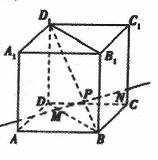
 各棱长都为a,p为线段
各棱长都为a,p为线段 上的动点.
上的动点. ;
; 的大小;
的大小;
 =2,
=2, ,
, ,且
,且 ,则
,则 ·
· +
+ +
+
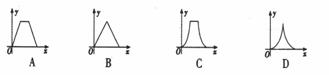
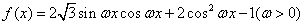 的图像上的一
的图像上的一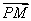 ·
·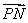 =16-
=16-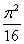
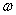 的值;
的值;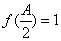 ,且a=2,b+c=4,
,且a=2,b+c=4, :函数
:函数 是最小正周期为
是最小正周期为 的周期函数,命题
的周期函数,命题 :函数
:函数 在
在 上单调递减,则下列命题为真命题的是
上单调递减,则下列命题为真命题的是 B.
B. C.
C. D.
D. 

 其中
其中 表示不超过
表示不超过 的最大整数,
的最大整数, ,
, ,
, ).若直线
).若直线 与函数
与函数 的图象恰有三个不同的交点,则实数
的图象恰有三个不同的交点,则实数 的取值范围是
的取值范围是  B.
B. C.
C.  D.
D.
 在
在 内有极小值的充分不必要条件是( )
内有极小值的充分不必要条件是( )


