题目内容
下列各命题中正确命题的序号是
①将f(x)=sin(2x+
)的图象向右平移
个单位长度,即得到函数y=sin2x的图象;
②命题“?x∈R,x2+1>3x”的否定是“?x∈R,x2+1≤3x”;
③“函数 f(x)=cos2ax-sin2ax的最小正周期为π”是“a=1”的必要不充分条件;
④“平面向量
与
的夹角是钝角”的充要条件是“
•
<0”.
①②③
①②③
①将f(x)=sin(2x+
| π |
| 4 |
| π |
| 8 |
②命题“?x∈R,x2+1>3x”的否定是“?x∈R,x2+1≤3x”;
③“函数 f(x)=cos2ax-sin2ax的最小正周期为π”是“a=1”的必要不充分条件;
④“平面向量
| a |
| b |
| a |
| b |
分析:利用函数的图象的平移判断①的正误;特称命题的否定判断②的正误;求出函数的周期判断③的正误;利用向量的数量积与夹角的关系判断④的正误.
解答:解:①将f(x)=sin(2x+
)的图象向右平移
个单位长度,即得到函数f(x)=sin[2(x-
)+
]=sin2x的图象;所以①正确;
②命题“?x∈R,x2+1>3x”的否定是“?x∈R,x2+1≤3x”;满足特称命题的否定是全称命题的形式,所以②正确;
③“函数 f(x)=cos2ax-sin2ax=cos2ax,它的最小正周期为π,所以
=π,所以a=±1”;
所以“函数 f(x)=cos2ax-sin2ax的最小正周期为π”是“a=1”的必要不充分条件;正确;
④“平面向量
与
的夹角是钝角”的充要条件是“
•
<0”.显然两个向量的夹角是π满足题意,所以判断不正确;
正确命题是①②③.
故答案为:①②③.
| π |
| 4 |
| π |
| 8 |
| π |
| 8 |
| π |
| 4 |
②命题“?x∈R,x2+1>3x”的否定是“?x∈R,x2+1≤3x”;满足特称命题的否定是全称命题的形式,所以②正确;
③“函数 f(x)=cos2ax-sin2ax=cos2ax,它的最小正周期为π,所以
| 2π |
| 2|a| |
所以“函数 f(x)=cos2ax-sin2ax的最小正周期为π”是“a=1”的必要不充分条件;正确;
④“平面向量
| a |
| b |
| a |
| b |
正确命题是①②③.
故答案为:①②③.
点评:本题考查基本知识的应用,涉及三角函数的图象的平移,特称命题与全称命题的否定关系,向量的数量积等知识,基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
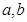 都是奇数,则
都是奇数,则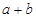 是偶数”的逆否命题是“若
是偶数”的逆否命题是“若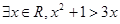 ”的否定是“
”的否定是“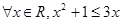 ” ;
” ;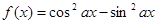 的最小正周期为
的最小正周期为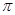 ” 是“
” 是“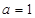 ”的必要不充分条件;
”的必要不充分条件;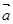 与
与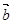 的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“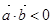 ” .
” . 的图象向右平移
的图象向右平移 个单位长度,即得到函数y=sin2x的图象;
个单位长度,即得到函数y=sin2x的图象; 与
与 的夹角是钝角”的充要条件是“
的夹角是钝角”的充要条件是“ ”.
”.