题目内容
14.在△ABC中,若$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$则$\overrightarrow{CA}$=( )| A. | $\overrightarrow{a}$ | B. | $\overrightarrow{a}$+$\overrightarrow{b}$ | C. | $\overrightarrow{b}$-$\overrightarrow{a}$ | D. | $\overrightarrow{a}$-$\overrightarrow{b}$ |
分析 根据平面向量的加减法运算,利用三角形法则得到所求.
解答 解:$\overrightarrow{CA}=\overrightarrow{CB}+\overrightarrow{BA}=-\overrightarrow{b}+\overrightarrow{a}=\overrightarrow{a}-\overrightarrow{b}$;
故选D.
点评 本题考查了平面向量的加减法运算;属于基础题.

练习册系列答案
相关题目
4.在△ABC中,已知其面积为S=a2-(b-c)2,则cosA=( )
| A. | $\frac{3}{4}$ | B. | $\frac{13}{15}$ | C. | $\frac{15}{17}$ | D. | $\frac{17}{19}$ |
5.已知一组数据为-3,5,7,x,11,且这组数据的众数为5,那么数据的中位数是( )
| A. | 7 | B. | 5 | C. | 6 | D. | 11 |
2.${∫}_{1}^{2}$$\frac{1}{x}$dx=( )
| A. | ln2 | B. | 2ln2 | C. | -ln2 | D. | 0 |
9.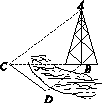 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=135°,CD=30m,并在点C处测得塔顶A的仰角为30°,则塔高AB
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=135°,CD=30m,并在点C处测得塔顶A的仰角为30°,则塔高AB
为( )
 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=135°,CD=30m,并在点C处测得塔顶A的仰角为30°,则塔高AB
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=135°,CD=30m,并在点C处测得塔顶A的仰角为30°,则塔高AB为( )
| A. | 10$\sqrt{2}$ m | B. | 10$\sqrt{3}$ m | C. | 15$\sqrt{6}$ m | D. | 10$\sqrt{6}$ m |
19.点M(3,-3,-1)关于xOy平面对称的点是( )
| A. | (-3,3,-1) | B. | (-3,-3,-1) | C. | (3,-3,1) | D. | (-3,3,1) |
6.(文)曲线y=x3-3x在点(2,2)的切线斜率是( )
| A. | -1 | B. | 6 | C. | -3 | D. | 9 |
3.已知函数f(x)=(2+x)2-3x,则f′(1)为( )
| A. | 6 | B. | 0 | C. | 3 | D. | 7 |