题目内容
8.已知A(2,0),O为坐标原点,动点P满足|$\overrightarrow{OP}$+$\overrightarrow{OA}$|+|$\overrightarrow{OP}$-$\overrightarrow{OA}$|=4$\sqrt{2}$(Ⅰ)求动点P的轨迹C的方程;
(Ⅱ)过点A且不垂直于坐标轴的直线l交轨迹C于不同的两点M,N,线段MN的垂直平分线与x轴交于点D,线段MN的中点为H,求$\frac{|DH|}{|MN|}$的取值范围.
分析 (Ⅰ)设P(x,y),由已知得$\sqrt{(x+2)^{2}+{y}^{2}}$+$\sqrt{(x-2)^{2}+{y}^{2}}$=$4\sqrt{2}$>4,由椭圆的定义可得所求轨迹方程;
(Ⅱ)设直线l的斜率为k(k≠0),M(x1,y1),N(x2,y2),则l的方程为y=k(x-2),将其代入椭圆方程,运用韦达定理和弦长公式,以及中点坐标公式,两点的距离公式,化简整理,运用不等式的性质,即可得到所求范围.
解答 解:(Ⅰ)设P(x,y),由已知得$\sqrt{(x+2)^{2}+{y}^{2}}$+$\sqrt{(x-2)^{2}+{y}^{2}}$=$4\sqrt{2}$>4,
根据椭圆定义知P点轨迹为以(2,0)和(-2,0)为焦点,长轴长为$4\sqrt{2}$的椭圆,
即有a=2$\sqrt{2}$,c=2,b=2,
则动点P的轨迹C的方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1;
(Ⅱ)设直线l的斜率为k(k≠0),M(x1,y1),N(x2,y2),
则l的方程为y=k(x-2),将其代入$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1,
整理得(1+2k2)x2-8k2x+8k2-8=0,
由于A在椭圆内,当然对任意实数k都有△>0,
根据韦达定理得x1+x2=$\frac{8{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{8{k}^{2}-8}{1+2{k}^{2}}$,
那么|MN|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{1+{k}^{2}}$•$\sqrt{(-\frac{8{k}^{2}}{1+2{k}^{2}})^{2}-\frac{32{k}^{2}-32}{1+2{k}^{2}}}$
=$\frac{4\sqrt{2}(1+{k}^{2})}{1+2{k}^{2}}$,
y1+y2=k(x1-2)+k(x2-2)=k(x1+x2)-4k=$\frac{-4k}{1+2{k}^{2}}$,
线段MN中点H的坐标为($\frac{4{k}^{2}}{1+2{k}^{2}}$,$\frac{-2k}{1+2{k}^{2}}$),
那么线段MN的垂直平分线方程为y+$\frac{2k}{1+2{k}^{2}}$=-$\frac{1}{k}$(x-$\frac{4{k}^{2}}{1+2{k}^{2}}$),
令y=0,得D($\frac{2{k}^{2}}{1+2{k}^{2}}$,0),
|DH|=$\sqrt{(\frac{2{k}^{2}}{1+2{k}^{2}})^{2}+(\frac{-2k}{1+2{k}^{2}})^{2}}$=$\frac{2\sqrt{{k}^{4}+{k}^{2}}}{1+2{k}^{2}}$,
则$\frac{|DH|}{|MN|}$=$\frac{2\sqrt{{k}^{4}+{k}^{2}}}{1+2{k}^{2}}$•$\frac{1+2{k}^{2}}{4\sqrt{2}(1+{k}^{2})}$=$\frac{\sqrt{2}}{4}$•$\frac{1}{\sqrt{1+\frac{1}{{k}^{2}}}}$,
由k≠0,可得1+$\frac{1}{{k}^{2}}$∈(1,+∞),
于是$\frac{|DH|}{|MN|}$∈(0,$\frac{\sqrt{2}}{4}$).
点评 本题考查椭圆的方程的求法,注意运用椭圆的定义的运用,考查直线方程和椭圆方程联立,运用韦达定理,以及弦长公式,中点坐标公式以及直线方程的运用,考查运算能力,属于中档题.

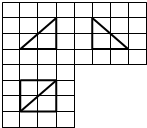 如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为( )
如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为( )| A. | 2 | B. | $2\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | 4 |
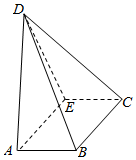 已知在底面为矩形的四棱锥D-ABCE中,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,二面角D-AE-C的平面角的正切值为-2.
已知在底面为矩形的四棱锥D-ABCE中,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,二面角D-AE-C的平面角的正切值为-2.