题目内容
设A、B两点在河的两岸，要测量两点之间的距离，测量者在A的同侧，在所在的河岸边选定一点C，测出AC的距离是55m，∠BAC=51°，∠ACB=75°．求A、B两点的距离（精确到0.1m）
根据正弦定理可知
=
∴AB=
=
=
≈65.7
答：A、B两点间的距离为65.7米
| AB |
| sin∠ACB |
| AC |
| sin∠ABC |
∴AB=
| ACsin∠ACB |
| sin∠ABC |
| 55sin70° |
| sin(180°-51°-75°) |
| 55sin70° |
| sin54° |
答：A、B两点间的距离为65.7米
练习册系列答案
名校课堂系列答案
相关题目
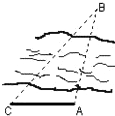如图，设A、B两点在河的两岸，一测量者在A的同侧，在所在的河岸边选定一点C，测出AC的距离为50m，∠ACB=45°，∠CAB=105°后，就可以计算出A、B两点的距离为（ ）A、50
| ||||
B、50
| ||||
C、25
| ||||
D、
|
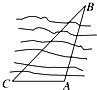如图，设A，B两点在河的两岸，一测量者在A的同侧，在A所在的河岸边选定一点C，测出AC的距离为50m，∠ACB=45°，∠CAB=105°后，则A，B两点的距离为
如图，设A，B两点在河的两岸，一测量者在A的同测，在所在的河岸边 选定一点C，测出AC的距离为50m，∠ACB=45°，∠CAB=105°后，就可以计 算出A，B两点的距离为（精确到0.1）（ ）
如图，设A、B两点在河的两岸，一测量者在A的同侧所在的河岸边选定一点C，测出AC的距离为50m，∠ACB=45°，∠CAB=105°后，就可以计算出A、B两点的距离为（ ）