题目内容
设A、B两点在河的两岸，要测量两点之间的距离，测量者在A的同侧，在所在的河岸边选定一点C，测出AC的距离是55m，∠BAC=51°，∠ACB=75°．求A、B两点的距离（精确到0.1m）分析：这是一道关于测量从一个可到达的点到一个不可到达的点之间的距离的问题，题目条件告诉了边AB的对角，AC为已知边，再根据三角形的内角和定理很容易根据两个已知角算出AC的对角，应用正弦定理算出AB边．
解答：解：根据正弦定理可知
=
∴AB=
=
=
≈65.7
答：A、B两点间的距离为65.7米
| AB |
| sin∠ACB |
| AC |
| sin∠ABC |
∴AB=
| ACsin∠ACB |
| sin∠ABC |
| 55sin70° |
| sin(180°-51°-75°) |
| 55sin70° |
| sin54° |
答：A、B两点间的距离为65.7米
点评：本题主要考查了解三角形的实际应用．考查了学生运用所学知识解决实际问题的能力．
练习册系列答案
阅读快车系列答案
相关题目
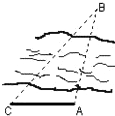如图，设A、B两点在河的两岸，一测量者在A的同侧，在所在的河岸边选定一点C，测出AC的距离为50m，∠ACB=45°，∠CAB=105°后，就可以计算出A、B两点的距离为（ ）A、50
| ||||
B、50
| ||||
C、25
| ||||
D、
|
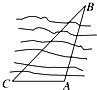如图，设A，B两点在河的两岸，一测量者在A的同侧，在A所在的河岸边选定一点C，测出AC的距离为50m，∠ACB=45°，∠CAB=105°后，则A，B两点的距离为
如图，设A，B两点在河的两岸，一测量者在A的同测，在所在的河岸边 选定一点C，测出AC的距离为50m，∠ACB=45°，∠CAB=105°后，就可以计 算出A，B两点的距离为（精确到0.1）（ ）
如图，设A、B两点在河的两岸，一测量者在A的同侧所在的河岸边选定一点C，测出AC的距离为50m，∠ACB=45°，∠CAB=105°后，就可以计算出A、B两点的距离为（ ）