题目内容
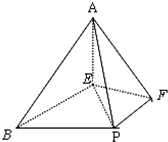 如图,在四棱锥A-BEFP中,AE⊥底面BEFP,BE⊥EF,∠EBP=
如图,在四棱锥A-BEFP中,AE⊥底面BEFP,BE⊥EF,∠EBP=| π | 3 |
(1)求直线AE与平面ABP所成角的大小;
(2)求二面角B-AP-F的余弦值.
分析:(1)建立空间直角坐标系,确定
=(0,0,-1),平面ABP的一个法向量
=(3,
,6),利用向量的夹角公式,可得结论;
(2)确定平面AFP、平面ABP的一个法向量,利用向量的夹角公式,即可得到结论.
| AE |
| n |
| 3 |
(2)确定平面AFP、平面ABP的一个法向量,利用向量的夹角公式,即可得到结论.
解答:解:(1)因为AE⊥底面BEFP,所以AE⊥BE,AE⊥EF,又BE⊥EF,所以AE,BE,EF三条直线两两垂直,以E为原点,EB,EF,EA分别为x轴,y轴,z轴建立如图所示的空间直角坐标系E-xyz,…..(2分)
在图2中,AE=1,BE=2,又AF=2,AE⊥EF,所以EF=
所以E
,A
,B
,F
,
又PB=2,∠EBP=
,所以P
…(4分)
∴
=(2,0,-1);
=(1,
,-1),
=(0,0,-1)
设
=(x,y,z)平面ABP的一个法向量,
∴
,∴
令x=3,则z=6,y=
,所以
=(3,
,6)…(6分)
设直线AE与平面ABP所成的角为θ,∴sinθ=
=
=
所以直线AE与平面ABP所成的角为60°….(8分)
(2)设
=(a,b,c)平面AFP的一个法向量
∴
=(0,
,-1);
=(1,
,-1),
,∴
∴a=0,令b=
,则c=3,得
=(0,
,3)….(10分)
∴cos<
,
>=
=
=
,….(12分)
因为二面角B-AP-F为钝角,所以二面角B-AP-F的大小余弦值为-
….(13分)
在图2中,AE=1,BE=2,又AF=2,AE⊥EF,所以EF=
| 3 |
所以E
|
|
|
|
又PB=2,∠EBP=
| π |
| 3 |
|
∴
| AB |
| AP |
| 3 |
| AE |
设
| n |
∴
|
|
令x=3,则z=6,y=
| 3 |
| n |
| 3 |

设直线AE与平面ABP所成的角为θ,∴sinθ=
|
| ||||
|
|
| 6 | ||
4
|
| ||
| 2 |
所以直线AE与平面ABP所成的角为60°….(8分)
(2)设
| m |
∴
| AF |
| 3 |
| AP |
| 3 |
|
|
∴a=0,令b=
| 3 |
| m |
| 3 |
∴cos<
| n |
| m |
| ||||
|
|
| 21 | ||||
4
|
| 7 |
| 8 |
因为二面角B-AP-F为钝角,所以二面角B-AP-F的大小余弦值为-
| 7 |
| 8 |
点评:本题考查线面角,考查面面角,考查利用向量知识解决空间角,解题的关键是确定平面法向量的坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
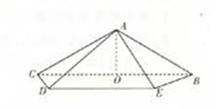
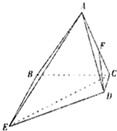 (2013•石家庄二模)如图,在四棱锥A-BCDE中,底面BCDE为直角梯形,且BE∥CD,CD⊥BC.侧面ABC⊥底面BCDE,F为AC的中点,BC=BE=4CD=2,AB=AC.
(2013•石家庄二模)如图,在四棱锥A-BCDE中,底面BCDE为直角梯形,且BE∥CD,CD⊥BC.侧面ABC⊥底面BCDE,F为AC的中点,BC=BE=4CD=2,AB=AC. =45
=45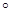 ,O是BC的中点,AO=
,O是BC的中点,AO= ,且BC=6,AD=AE=2CD=2
,且BC=6,AD=AE=2CD=2 ,
,
 ,AE=1,BE=FA=PB=2.
,AE=1,BE=FA=PB=2.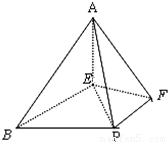
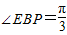 ,AE=1,BE=FA=PB=2.
,AE=1,BE=FA=PB=2.