题目内容
已知动点P在曲线2x2-y=0上移动,则点A(0,-1)与点P连线中点的轨迹方程是A.y=2x2 B.y=8x2 C.2y=8x2-1 D.2y=8x2+1
C 设P(x0,y0),设PA的中点为Q(x,y),
则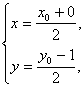 ∴
∴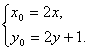 ∴P(2x,2y+1).又点P在曲线2x2-y=0上,
∴P(2x,2y+1).又点P在曲线2x2-y=0上,
代入,得2(2x)2-2y-1=0,即8x2-2y-1=0,∴2y=8x2-1.

练习册系列答案
相关题目
题目内容
已知动点P在曲线2x2-y=0上移动,则点A(0,-1)与点P连线中点的轨迹方程是A.y=2x2 B.y=8x2 C.2y=8x2-1 D.2y=8x2+1
C 设P(x0,y0),设PA的中点为Q(x,y),
则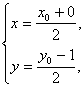 ∴
∴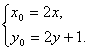 ∴P(2x,2y+1).又点P在曲线2x2-y=0上,
∴P(2x,2y+1).又点P在曲线2x2-y=0上,
代入,得2(2x)2-2y-1=0,即8x2-2y-1=0,∴2y=8x2-1.
