题目内容
= ．
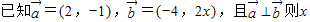【答案】分析：由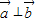
，可得
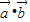=0，即2×（-4）-2x=0，解之即可．
解答：解：∵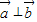
，∴
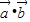=0，
即2×（-4）-2x=0，
解得x=-4，
故答案为：-4
点评：本题考向量的坐标运算和向量垂直的充要条件，属基础题．
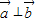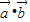，可得=0，即2×（-4）-2x=0，解之即可．解答：解：∵
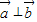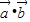，∴=0，即2×（-4）-2x=0，
解得x=-4，
故答案为：-4
点评：本题考向量的坐标运算和向量垂直的充要条件，属基础题．
练习册系列答案
相关题目
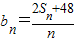，数列bn的最小项是第几项，并求出该项的值．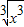
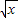）2
有公共焦点，且离心率是
的双曲线方程，并求其渐近线方程．
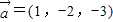则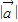
=（ ）
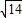
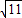
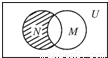设全集U是实数集R，M={x|x2＞4}，N={x|1＜x≤3}，则图中阴影部分表示的集合是（ ）
