题目内容
已知函数f(x)的定义域为(0,+∞),且满足条件:①f=f(x)+f(y) ②f(2)=1 ③当x>1时,f(x)>0
(1)求f(1)的值;
(2)讨论函数f(x)的单调性;
(3)求满足f(x)+f(2x)≤2的x的取值范围.
【答案】分析:(1)在①中令x=y=1,可由f(x•y)=f(x)+f(y),求出f(1)的值
(2)在①中令y=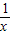 ,结合(1)中f(1)=0,当x>1时,f(x)>0,分析f(x2)-f(x1)的符号,结合函数单调性的定义,可得答案.
,结合(1)中f(1)=0,当x>1时,f(x)>0,分析f(x2)-f(x1)的符号,结合函数单调性的定义,可得答案.
(3)由f(2)=1,可得2=f(4),结合(2)中函数的单调性,可将不等式f(x)+f(2x)≤2,转化为不等式组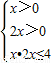 ,解得x的取值范围.
,解得x的取值范围.
解答:解:(1)在①中令x=y=1,得f(1)=f(1)+f(1)故 f(1)=0 …(2分)
(2)在①中令y=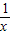 ,得f(1)=f(x)+f(
,得f(1)=f(x)+f(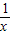 )=0
)=0
即f(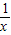 )=-f(x),
)=-f(x),
函数f(x)在(0,+∞)上的单调递增,理由如下:
任取x1,x2,设x2>x1>0,
∴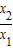 >1
>1
∵当x>1时,f(x)>0
∴f(x2)-f(x1)=f(x2)+f(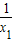 )=f(
)=f(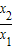 )>0 …(6分)
)>0 …(6分)
f(x2)>f(x1),
∴f(x)在(0,+∞)上是增函数,…(8分)
(3)由f(2)=1,得2f(2)=2=f(2)+f(2)=f(4)…(9分)
∴f(x)+f(2x)≤2可化为
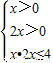
解得0<x≤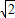 .…(12分)
.…(12分)
点评:本题考查的知识点是抽象函数及其应用,其中熟练掌握抽象函数的解答方法是解答的关键.
(2)在①中令y=
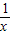 ,结合(1)中f(1)=0,当x>1时,f(x)>0,分析f(x2)-f(x1)的符号,结合函数单调性的定义,可得答案.
,结合(1)中f(1)=0,当x>1时,f(x)>0,分析f(x2)-f(x1)的符号,结合函数单调性的定义,可得答案.(3)由f(2)=1,可得2=f(4),结合(2)中函数的单调性,可将不等式f(x)+f(2x)≤2,转化为不等式组
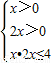 ,解得x的取值范围.
,解得x的取值范围.解答:解:(1)在①中令x=y=1,得f(1)=f(1)+f(1)故 f(1)=0 …(2分)
(2)在①中令y=
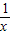 ,得f(1)=f(x)+f(
,得f(1)=f(x)+f(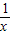 )=0
)=0即f(
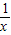 )=-f(x),
)=-f(x),函数f(x)在(0,+∞)上的单调递增,理由如下:
任取x1,x2,设x2>x1>0,
∴
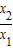 >1
>1∵当x>1时,f(x)>0
∴f(x2)-f(x1)=f(x2)+f(
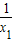 )=f(
)=f(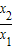 )>0 …(6分)
)>0 …(6分)f(x2)>f(x1),
∴f(x)在(0,+∞)上是增函数,…(8分)
(3)由f(2)=1,得2f(2)=2=f(2)+f(2)=f(4)…(9分)
∴f(x)+f(2x)≤2可化为
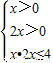
解得0<x≤
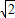 .…(12分)
.…(12分)点评:本题考查的知识点是抽象函数及其应用,其中熟练掌握抽象函数的解答方法是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
