题目内容
19.已知函数y=sinxcosx.(1)要得到函数y=-sin2x+$\frac{1}{2}$的图象,需将y=sinxcosx的图象怎么变换得到?
(2)把y=sinxcosx的图象向右平移$\frac{π}{6}$个单位,得到g(x)的图象,求g(x)的解析式,并用“五点法”作出它在一个周期内的图象.
分析 (1)将2个函数用二倍角公式化简,根据函数y=Asin(ωx+φ)的图象变换规律即可解决.
(2)由函数y=Asin(ωx+φ)的图象变换可得g(x)的解析式,用“五点法”即可作出它在一个周期内的图象.
解答 解:(1)∵函数y=-sin2x+$\frac{1}{2}$=$\frac{1}{2}$cos2x,
又∵y=sinxcosx=$\frac{1}{2}$sin2x=$\frac{1}{2}$cos(2x+$\frac{π}{2}$),
∴只需将y=sinxcosx=$\frac{1}{2}$sin2x=$\frac{1}{2}$cos(2x+$\frac{π}{2}$)的图象向右平移$\frac{π}{4}$个单位即可得到函数y=-sin2x+$\frac{1}{2}$=$\frac{1}{2}$cos2x的图象.
(2)把y=sinxcosx=$\frac{1}{2}$sin2x的图象向右平移$\frac{π}{6}$个单位,得到g(x)=$\frac{1}{2}$sin[2(x-$\frac{π}{6}$)]=$\frac{1}{2}$sin(2x-$\frac{π}{3}$).
列表:
| 2x-$\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ | $\frac{7π}{6}$ |
| y=$\frac{1}{2}$sin(2x-$\frac{π}{3}$) | 0 | $\frac{1}{2}$ | 0 | -$\frac{1}{2}$ | 0 |
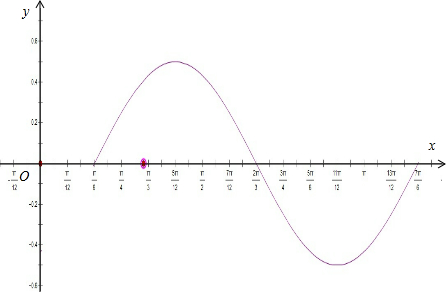
点评 本题主要考察二倍角公式的应用和函数y=Asin(ωx+φ)的图象变换,考查了五点作图法的应用,属于基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
10.已知某工厂生产的一种零件内径尺寸服从正态分布N(22.5,0.12),则该零件尺寸大于22.5的概率为( )
| A. | 0.01 | B. | 0.1 | C. | 0.5 | D. | 0.9 |
14.将函数y=2sin(3x+$\frac{π}{6}$)的图象向右平移$\frac{π}{3}$个单位,所的图象对应的函数( )
| A. | 在[-$\frac{π}{9}$,$\frac{2π}{9}$]上单调递增 | B. | 在[-$\frac{π}{9}$,$\frac{2π}{9}$]上单调递减 | ||
| C. | 在[$\frac{π}{9}$,$\frac{4π}{9}$]上单调递增 | D. | 在[$\frac{π}{9}$,$\frac{4π}{9}$]上单调递减 |
11.已知命题p:复数$\frac{a+i}{1+i}$(a∈R,i为虚数单位)在复平面上对应的点在第二象限,命题q:曲线y=x2+(2a-3)•x+1与x轴没有交点.若“p∨q”为真,则实数a的取值范围为( )
| A. | (-∞,$\frac{1}{2}$)∪($\frac{5}{2}$,+∞) | B. | (-∞,-1)∪($\frac{1}{2}$,$\frac{5}{2}$) | C. | (-∞,-1)∪[$\frac{1}{2}$,$\frac{5}{2}$] | D. | (-∞,$\frac{1}{2}$]∪[$\frac{5}{2}$,+∞) |
8.若函数y=($\frac{1}{2}$)x-1+m的图象不经过第一象限,则m的取值范围是( )
| A. | m≥-1 | B. | m≥-2 | C. | m≤-1 | D. | m≤-2 |