题目内容
8.函数$f(x)=\sqrt{{{log}_{\frac{1}{3}}}(4x-5)}$的定义域为( )| A. | $(\frac{5}{4},+∞)$ | B. | $(-∞,\frac{5}{4})$ | C. | $(\frac{5}{4},\frac{3}{2}]$ | D. | $(\frac{5}{4},\frac{3}{2})$ |
分析 根据函数f(x)的解析式,列出使解析式有意义的不等式,求出解集即可.
解答 解:∵函数$f(x)=\sqrt{{{log}_{\frac{1}{3}}}(4x-5)}$,
∴${log}_{\frac{1}{3}}$(4x-5)≥0,
∴0<4x-5≤1,
即5<4x≤6;
解得$\frac{5}{4}$<x≤$\frac{3}{2}$,
∴函数f(x)的定义域为($\frac{5}{4}$,$\frac{3}{2}$].
故选:C.
点评 本题考查了求函数定义域的应用问题,也考查了对数函数的图象与性质的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.满足BC=1.5,AC=1,B=30°的不同△ABC有多少个( )
| A. | 两个 | B. | 一个 | C. | 零个 | D. | 无数个 |
13.设等差数列{an}的公差是d,其前项和是Sn,若a1=d=1,则$\frac{{S}_{n}+8}{{a}_{n}}$的最小值是( )
| A. | $\frac{9}{2}$ | B. | $\frac{7}{2}$ | C. | 2$\sqrt{2}$+$\frac{1}{2}$ | D. | 2$\sqrt{2}$-$\frac{1}{2}$ |
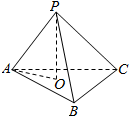 三棱锥P-ABC中,PO⊥面ABC,垂足为O,若PA⊥BC,PC⊥AB,求证:
三棱锥P-ABC中,PO⊥面ABC,垂足为O,若PA⊥BC,PC⊥AB,求证: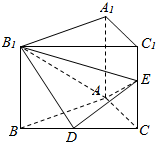 如图,在直三棱柱ABC-A1B1C1中,D,E分别是BC和CC1的中点,已知AB=AC=AA1=4,∠BAC=90°.
如图,在直三棱柱ABC-A1B1C1中,D,E分别是BC和CC1的中点,已知AB=AC=AA1=4,∠BAC=90°.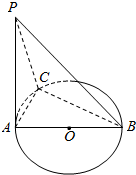 AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点.
AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点.