题目内容
函数y=sin2x+2cosx(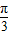 ≤x≤
≤x≤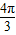 )的最小值为 .
)的最小值为 .
【答案】分析:先将y=sin2x+2cosx转化为y=-cos2x+2cosx+1,再配方,利用余弦函数的单调性求其最小值.
解答:解:∵y=sin2x+2cosx
=-cos2x+2cosx+1
=-(cosx-1)2+2,
∵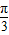 ≤x≤
≤x≤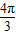 ,
,
∴-1≤cosx≤ ,-2≤cosx-1≤-
,-2≤cosx-1≤- ,
,
∴ ≤(cosx-1)2≤4,-4≤-(cosx-1)2≤-
≤(cosx-1)2≤4,-4≤-(cosx-1)2≤- .
.
∴-2≤2-(cosx-1)2≤ .
.
∴函数y=sin2x+2cosx(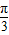 ≤x≤
≤x≤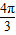 )的最小值为-2.
)的最小值为-2.
故答案为:-2.
点评:本题考查余弦函数的单调性,考查转化思想与配方法的应用,属于中档题.
解答:解:∵y=sin2x+2cosx
=-cos2x+2cosx+1
=-(cosx-1)2+2,
∵
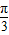 ≤x≤
≤x≤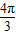 ,
,∴-1≤cosx≤
 ,-2≤cosx-1≤-
,-2≤cosx-1≤- ,
,∴
 ≤(cosx-1)2≤4,-4≤-(cosx-1)2≤-
≤(cosx-1)2≤4,-4≤-(cosx-1)2≤- .
.∴-2≤2-(cosx-1)2≤
 .
.∴函数y=sin2x+2cosx(
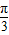 ≤x≤
≤x≤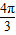 )的最小值为-2.
)的最小值为-2.故答案为:-2.
点评:本题考查余弦函数的单调性,考查转化思想与配方法的应用,属于中档题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目