题目内容

函数y=sin2x的图象在点P(
π
6
，
1
4
)处的切线的斜率是
3
2
3
2
．
分析：求出函数y=sin2x在x=
π
6
处的导数值，这个导数值即函数图象在该点处的切线的斜率．
解答：解：因为函数y=sin2x，所以导函数y′=2sinxcosx=sin2x，
函数y=sin2x的图象在点P(
π
6
，
1
4
)处的切线的斜率y′
|
 
x=
π
6
=sin
π
3
=
3
2

故答案为：
3
2
点评：本题主要考查了利用导数研究曲线上某点切线方程，解题的关键是求函数的导数，属于基础题．
练习册系列答案
相关题目
（2012•山东）设命题p：函数y=sin2x的最小正周期为
π
2
；命题q：函数y=cosx的图象关于直线x=
π
2
对称．则下列判断正确的是（　　）
给出下列命题：①存在实数x，使sinx+cosx=
3
2
；
②若α，β是第一象限角，且α＞β，则cosα＜cosβ；
③函数y=sin(
2
3
x+
π
2
)是偶函数；
④函数y=sin2x的图象向左平移
π
4
个单位，得到函数y=sin(2x+
π
4
)的图象．
其中正确命题的序号是
 
．（把正确命题的序号都填上）
要得到函数y=sin2x的图象，可由函数y=cos(2x-
π4
)（　　）
（2011•许昌三模）为得到函数y=cos(2x+
π
3
)的图象，只需将函数y=sin2x的图象（　　）
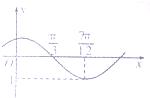（2013•蚌埠二模）已知函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜
π2
）的图象如图所示．
（I） 求函数f（x）的解析式；
（II）如何通过变换函数f（x）的图象得到函数y=sin2x的图象？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网