题目内容
8.现有$\frac{n(n+1)}{2}$(n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵:
设Mk是第k行中的最大数,其中1≤k≤n,k∈N*.记M1<M2<…<Mn的概率为pn.
(1)求p2的值;
(2)证明:pn>$\frac{{C}_{n+1}^{2}}{(n+1)!}$.
分析 (1)由题意知p2=$\frac{2{A}_{2}^{2}}{{A}_{3}^{3}}$=$\frac{2}{3}$,
(2)先排第n行,则最大数在第n行的概率为$\frac{n}{\frac{n(n+1)}{2}}$=$\frac{2}{n+1}$,即可求出为pn,再根据二项式定理和放缩法即可证明.
解答 解:(1)由题意知p2=$\frac{2{A}_{2}^{2}}{{A}_{3}^{3}}$=$\frac{2}{3}$,即p2的值为 $\frac{2}{3}$.
(2)先排第n行,则最大数在第n行的概率为$\frac{n}{\frac{n(n+1)}{2}}$=$\frac{2}{n+1}$;
去掉第n行已经排好的n个数,
则余下的$\frac{n(n+1)}{2}$-n=$\frac{n(n-1)}{2}$个数中最大数在第n-1行的概率为$\frac{n}{\frac{n(n-1)}{2}}$=$\frac{2}{n}$;
…
故pn=$\frac{2}{n+1}$×$\frac{2}{n}$×…×$\frac{2}{3}$=$\frac{{2}^{n-1}}{(n+1)×n×…×3}$=$\frac{{2}^{n}}{(n+1)!}$.
由于2n=(1+1)n=Cn0+Cn1+Cn2+…+Cnn≥Cn0+Cn1+Cn2>Cn1+Cn2=Cn+12,
故$\frac{{2}^{n}}{(n+1)!}$>$\frac{{C}_{n+2}^{2}}{(n+1)!}$,即pn>$\frac{{C}_{n+1}^{2}}{(n+1)!}$.
点评 本题考查了排列组合的问题,以及二项式定理和放缩法证明不等式成立的问题,属于中档题

练习册系列答案
相关题目
18.“|x+1|+|x-2|≤5”是“-2≤x≤3”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.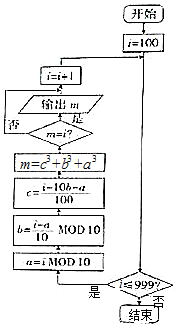 运行如图所示的程序框图,输出的数称为“水仙花数”.(算术符号MOD表示取余数,如11MOD2=1).下列数中的“水仙花数”是( )
运行如图所示的程序框图,输出的数称为“水仙花数”.(算术符号MOD表示取余数,如11MOD2=1).下列数中的“水仙花数”是( )
①“水仙花数”是三位数;
②152是“水仙花数”;
③407是“水仙花数”.
 运行如图所示的程序框图,输出的数称为“水仙花数”.(算术符号MOD表示取余数,如11MOD2=1).下列数中的“水仙花数”是( )
运行如图所示的程序框图,输出的数称为“水仙花数”.(算术符号MOD表示取余数,如11MOD2=1).下列数中的“水仙花数”是( )①“水仙花数”是三位数;
②152是“水仙花数”;
③407是“水仙花数”.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
13.在等差数列{an}中,2a7=a9+7,则数列{an}的前9项和S9=( )
| A. | 21 | B. | 35 | C. | 63 | D. | 126 |
18.设集合M={x∈R|x2<4},N={-1,1,2},则M∩N=( )
| A. | {-1,1,2} | B. | {-1,2} | C. | {1,2} | D. | {-1,1} |
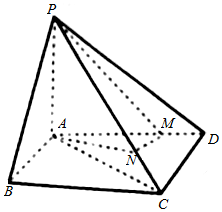 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,BC=AP=5,AB=3,AC=4,M,N分别在线段AD,CP上,且$\frac{AM}{MD}$=$\frac{PN}{NC}$=4.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,BC=AP=5,AB=3,AC=4,M,N分别在线段AD,CP上,且$\frac{AM}{MD}$=$\frac{PN}{NC}$=4. 已知三棱柱ABC-A1B1C1中,AB=AC=AA1=2,侧面ABB1A1⊥底面ABC,D是BC的中点,∠BAA1=120o,B1D⊥AB.
已知三棱柱ABC-A1B1C1中,AB=AC=AA1=2,侧面ABB1A1⊥底面ABC,D是BC的中点,∠BAA1=120o,B1D⊥AB.